2

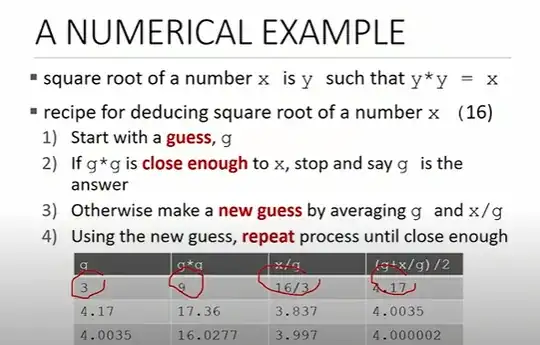
I was watching a video lecture from the series Introduction to Computer Science and Programming using Python (see here). It presents an algorithm for computing the square root of a number $x$. It starts with an initial guess $g$, and then taking the average $$\frac{g+\tfrac xg}{2},$$ and repeating. Why did they not take a simple average like $\frac{g+x}{2}$? Here is a screenshot:

Screenshot

Also Any resources which can help to improve my math's understanding related to tackling kind of math problems would also be really helpful

Servaes
  • 67,306
  • 8
  • 82
  • 171
Venkatesh Chauhan
  • 21
  • 1
  • I'm not sure what you're asking here. Note that $$ \frac{ g+ \frac{x}{g} }{2} \neq g + \frac{x}{2} $$ Anyway, the formula used is technically not the square root, but rather an iterative way to approach the square root with Newton's method. – Matti P. Aug 23 '21 at 10:00
  • Explaining it with simple words, $g$ and $\frac{x}{g}$ are things in the same order of magnitude than the square root $\sqrt x$. That is why it makes sense to take the average of $g$ and $\frac{x}{g}$. It wouldn't make sense to take the average of $g$ and $x$, as you suggest, since they could be too far apart from each other ($g$ is near $\sqrt x$ and $x$ isn't). – Miguel Mars Aug 23 '21 at 10:01
  • 1
    This algorithm is known as the "Babylonian method" for finding square roots. – Jean Marie Aug 23 '21 at 10:23
  • Thank you so much @Jean Marie and Matti P. . I will further try to understand the context as i am finding little hard to understand the text presented by others. If anyone can suggest me any supplementary reading , that would also be very helpful – Venkatesh Chauhan Aug 23 '21 at 10:30
  • @PM 2Ring What that would mean ? Idk but feeling little hard in comprehending this level of math's – Venkatesh Chauhan Aug 23 '21 at 10:42
  • Does this help? https://math.stackexchange.com/a/2386359/207316 – PM 2Ring Aug 23 '21 at 10:58

2 Answers2

3

Without any sophisticated theory, the point is that if $g>0$ and $g \neq \sqrt{x}$ then $g$ and $x/g$ are on opposite sides of $\sqrt{x}$, since they multiply together to give $x$. Therefore if the distance between $g$ and $\sqrt{x}$ is about the same as the distance between $x/g$ and $\sqrt{x}$, then the average of the two of them is going to be closer to $\sqrt{x}$ than either of them is.

You can check that $\frac{x}{g}-\sqrt{x}=-\frac{\sqrt{x}}{g}(g-\sqrt{x})$, so the condition I just mentioned basically amounts to "$\frac{\sqrt{x}}{g}$ is reasonably close to $1$". When this isn't true, things can get worse for one iteration and can then take a while to recover. For example, if you want $\sqrt{1}$ and you guess $10^{-12}$ then it's going to take about 40 iterations just to shrink your guess down to the right order of magnitude after it skyrockets to about $\frac{10^{12}}{2}$ in the first step.

Ian
  • 104,572
2

Because repeatedly taking the average $\frac{g+\tfrac{x}{g}}{2}$ converges to the square root, whereas repeatedly taking the average $\frac{g+x}{2}$ does not.

Servaes
  • 67,306
  • 8
  • 82
  • 171