I think this problem is easier if it's translated to $\mathbb{R}^2$. Let $\langle\cdot,\cdot\rangle$ be the the Euclidean inner product on $\mathbb{R}^2$, and as stated in the question, let $E$ be a line, and for now assume $E$ passes through the origin, and $A$ a point, with coordinates $\mathbf{a}$. Let $\mathbf{v}$ be a unit normal vector to $E$, then the reflection of $A$ in the line $E$ has coordinates $\mathbf{a}'$ given by $$\mathbf{a}'=\mathbf{a}-2\langle\mathbf{a},\mathbf{v}\rangle\mathbf{v}.$$ To understand why, notice that $\langle\mathbf{a},\mathbf{v}\rangle$ is the (signed) perpendicular distance between $A$ and $E$, so $\mathbf{a}-\langle\mathbf{a},\mathbf{v}\rangle\mathbf{v}$ would be the projection of $A$ to $E$, and $\mathbf{a}-2\langle\mathbf{a},\mathbf{v}\rangle\mathbf{v}$ is the point perpendicularly opposite $A$ across $E$. Hopefully this diagram helps illustrate this:
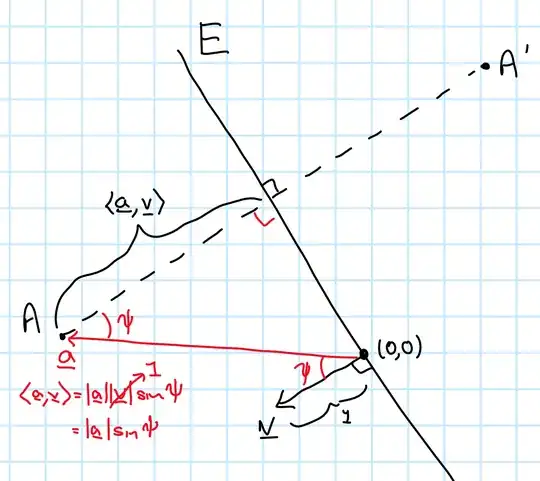
Now we just need to translate from the complex picture to the real picture and back again. Suppose $E$ is given by the complex equation $z=tw$, where $t$ is a real parameter, and $w$ is a fixed complex number (recall we assumed that $E$ passes through $0$). Writing $w=x+\mathrm{i}y$, the unit vector $\mathbf{v}$ has coodsinates $$\frac{1}{\sqrt{x^2+y^2}}(y,-x).$$ Now, if $\mathbf{a}$ as a complex number is $\alpha+\mathrm{i}\beta$, we can use the above expression to write $\mathbf{a}'$ as a complex number: $$\alpha+\mathrm{i}\beta-2\frac{1}{x^2+y^2}(\alpha y-\beta x)(y-\mathrm{i} x).$$
The only thing left to do is remove the assumption that $E$ passes through $0$. In general $E$ will be given by a complex equation $z=tw+w'$ where $w'$ is another fixed complex number. To get a reflection in this line, first translate the whole plane by $-w'$ so that $E$ passes through the origin, then apply the formula above, then translate the whole plane back by $w'$.
Edit:
It was pointed out in the comments that the asker wanted a description of affine reflections, not just orthogonal reflections. The answer above can be easily modified to to this more general setting by observing that any affine reflection in a line $E$ through the origin is conjugate to an orthogonal reflection in that line by an element of $\mathrm{GL}_2(\mathbb{R})$ which fixes the line. in only two dimensions it should be straightforward to compute the matrix of the conjugating transformation and apply it in the procedure above.
