Let finite number of $x_i$'s be reals. Define matrix $M_{ij} = \sqrt{|x_i+x_j|} - \sqrt{|x_i-x_j|}$. Is this matrix positive semidefinite?
I am reading this year's IMO problem number 2, which would be trivially true if we prove that $M_{ij}$ is positive semidefinite.
Problem $\boldsymbol2$. Show that the inequality $$\sum_{i=1}^{n}\sum_{j=1}^{n}\sqrt{\left|x_i - x_j\right|} \leqslant \sum_{i=1}^{n}\sum_{j=1}^n\sqrt{\left|x_i + x_j\right|}$$ holds for all real numbers $x_1,...,x_n$.
Define $f(x, y) = \sqrt{|x + y|} - \sqrt{|x-y|}$. Then we want to prove that \begin{align*} \mathbb{E}[f(X, Y)] \ge 0 \end{align*} where $X, Y$ independent and uniformly distributed over the set of values $\{x_1, \cdots, x_n\}$.
[Remark 1: I know the IMO is motivated to use techniques only available at the secondary school level, but the probabilistic notation allows me to naturally represent a bunch of summation notations in a succinct form, and can be translated easily to the summation notation in the original problem.]
First, let's observe the region in the Cartesian plane where $f(x, y) \ge a$ and $f(x, y) \le -a$, respectively:
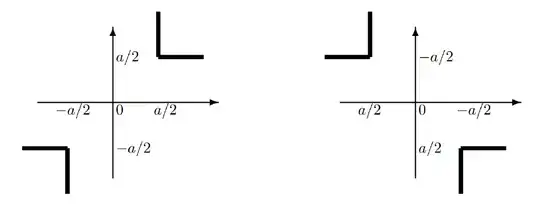
And therefore \begin{align*} \mathbb{P}(f(X, Y) \ge a) &= \mathbb{P}\left(X \ge \frac{a}{2}, Y \ge \frac{a}{2}\right) + \mathbb{P}\left(X \le -\frac{a}{2}, Y \le -\frac{a}{2}\right) \\ &= \mathbb{P}\left(X \ge \frac{a}{2}\right)^2 + \mathbb{P}\left(X \le -\frac{a}{2}\right)^2 \end{align*} and \begin{align*} \mathbb{P}(f(X, Y) \le a) &= \mathbb{P}\left(X \ge \frac{a}{2}, Y \le -\frac{a}{2}\right) + \mathbb{P}\left(X \le -\frac{a}{2}, Y \ge \frac{a}{2}\right) \\ &= 2\mathbb{P}\left(X \ge \frac{a}{2}\right) \left(X \le -\frac{a}{2}\right) \end{align*} Then, we need the lemma that \begin{align*} \mathbb{E}[A] = \int_0^\infty [\mathbb{P}(A \ge a) - \mathbb{P}(A \le -a)]da \end{align*}
which can be proved by noticing that $\mathbb{E}[A] = \mathbb{E}[A^+] - \mathbb{E}[A^-]$, where $A^+ = \max(A, 0)$ and $A^- = -\min(A, 0)$ and then applying the proof for the tail sum formula. Letting $A = f(X, Y)$,
\begin{align*} \mathbb{E}[f(X, Y)] &= \int_0^\infty[\mathbb{P}(f(X, Y) \ge a) - \mathbb{P}(f(X, Y) \le -a)]da \\ &= \int_0^\infty\left[\mathbb{P}\left(X \ge \frac{a}{2}\right) - \mathbb{P}\left(X \le -\frac{a}{2}\right)\right]^2da \\ &\ge 0 \end{align*}
Remark 2: Note this proof works for any $f(x, y) = g(|x+y|) - g(|x - y|)$ for non-decreasing $g: \mathbb{R}_{\ge 0} \rightarrow \mathbb{R}$ and general distributions for $X, Y$. For example, we also have the result \begin{align*} \sum_{i,j} w_i w_j \log(1 + |x_i - x_j|) \le \sum_{i,j} w_i w_j \log(1 + |x_i + x_j|) \end{align*} for weights $w_1, \cdots, w_n \ge 0$.
Remark 3: Completely forgot to answer the original problem. Note that if we choose $g(x) = \sqrt{x}$ and define $X, Y$ to be random variables distributed over $x_1, \cdots, x_n$ with weights $w_1, \cdots, w_n \ge 0$, then we effectively get, for $\mathbf{M} = [M_{ij}]_{ij}$, \begin{align*} \mathbf{w}^\intercal \mathbf{M}\mathbf{w} \ge 0 \end{align*} for $\mathbf{w} \in \mathbb{R}^n_{\ge 0}$; we need $\mathbf{w} \in \mathbb{R}^n$ in order to get genuine positive semidefiniteness. But it appears that if we replace $\mathbb{P}$ with quasiprobability distribution (e.g. negative measures are allowed), everything in the proof still seems to go through.
We will use an integral formula (there is a similar one for other constants in $(0,1)$ instead of $1/4$)
$$|s|^{\frac{1}{2}}= (s^2)^{\frac{1}{4}} = \frac{1}{4 \Gamma(\frac{3}{4})}\cdot \int_{0}^{\infty}\frac{1-e^{-s^2 t} }{t^{\frac{5}{4}}}\, d t$$
valid for every $s\in \mathbb{R}$. We conclude that we have
$$\sqrt{\|x_i+x_j\|}-\sqrt{\|x_i-x_j\|}= c\cdot \int_{0}^{\infty}\frac{e^{-t\|x_i-x_j\|^2}- e^{-t\|x_i+x_j\|^2}}{t^{\frac{5}{4}}}\, d t $$
But note that each $t\ge 0$ the matrix
$$M = M_t =(e^{-t\|x_i-x_j\|^2}- e^{-t\|x_i+x_j\|^2})_{i,j}$$
equals $D \cdot N \cdot D$, where $D$ is the matrix with diagonal elements $e^{-t \|x_i\|^2}$, and $N$ is the matrix $(2 \cosh(2 t \langle x_i, x_j \rangle)$. Now $(\langle x_i , x_j\rangle)$ is positive semidefinite, and so will be any componentwise function that has a positive series expansion (like for instance $\cosh( 2t\cdot )$ for $t\ge 0$). We conclude that $N$ is positive definite for all $t \ge 0$, and so will be $M_t$. We now use the fact that the psd matrices form a positive cone.
Note: The solution of Sangchul Lee using the cosine transform works better, with a direct calculation.
