0

I'm pretty sure this is a relatively straightforward and simple thing, but here we are.

I'm trying to write out (and use) the equation for the imaginary portion (kei(x)) of a zeroth order Kelvin function in order to plot out a graph similar to this, provided by Wikipedia. Wikipedia provides this equation as follows: 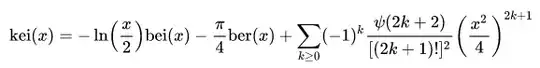kei(x)

It looks like to use this equation I simply need three things:

  1. An arbitrary value for the upper limit of the summation series
  2. The real part of the Bessel function bei(x)
  3. The imaginary part of the Bessel function ber(x)

This makes it seem like all I really need to do is to stuff the equations for (2) and (3) into the kei(x) equation. Wikipedia has again kindly provided these two equations: 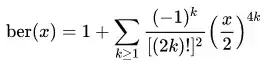ber(x) and bei(x)

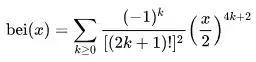
However, my attempts to code this (in MATLAB, though it shouldn't matter) has not yielded anything remotely close to the graph in question. I checked for different values of the upper limit of k.

Just wanted to check if my work process seems correct here. If it is, this just means my code in MATLAB is wrong and I can focus my efforts in finding it there. My code in question is here, if anyone is interested. Notably my graph of x vs kei(x) yields different results when I take a different upper limit of k.

Thanks everyone.

user825535
  • 25

2 Answers2

1

We can easily find the number $p$ of terms to be added for the computation of $$\text{ber}_0(x)=1+\sum_{k=1}^p (-1)^k \frac{1}{[(2 k)!]^2}\left(\frac{x}{2}\right)^{4 k}$$ in order to have $$\frac{1}{[(2 p+2)!]^2}\left(\frac{x}{2}\right)^{4 (p+4)} \leq 10^{-n}$$ that is to say $$\frac{1}{(2 p+2)!}\left(\frac{x}{2}\right)^{2 (p+4)} \leq 10^{-\frac n2}\implies(2p+2)! \geq \left(\frac{x}{2}\right)^{2p+2}\left(\frac{x}{2}\right)^{6 }10^{\frac n2}$$

If you look at this question of mine, the superb approximation proposed by @robjohn would give for this case

$$p \geq \frac{x}{4} \, e^{1+W(t)}-\frac{5}{4} \qquad \text{with} \qquad t=\frac 1{e x}\log \left(\frac{ 10^n}{2^{12} \pi }x^{11}\right)$$

If we make $x=10$ and $n=12$, this gives $p=13.1847$ so $\lceil p\rceil=14$.

Checking : for $p=13$ we have $3.64\times 10^{-12} >10^{-12}$ while for $p=14$, $3.01\times 10^{-15} <10^{-12}$. So, the result is correct.

Notice that the exact solution is $p=13.1851$.

Claude Leibovici
  • 289,558
0

No idea what I did, but I restarted from scratch and just rewrote the code. It works now. The more important thing I've learned is that the number of terms you consider for the upper limit of the infinite series expansion is very important; it appears that given an infinite number of terms the function wants to converge to 0 beyond x = 6 as can be shown in the graph. At, say, x = 60, considering 10 terms yields a value with a magnitude in the order of e22. Considering 50 terms puts it in the order of e8, and so on and so forth.

TLDR: The approach I outlined is correct, but an arbitrary number of terms needs to be "carefully" considered or else convergence will not be met.

user825535
  • 25