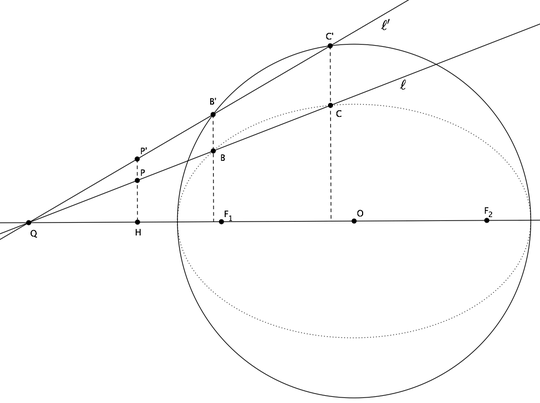
We are given three points: $F_1, F_2$ that are the two foci of the ellipse $\mathcal E$ and point $A$ that belongs to $\mathcal E$.
We are also given a random line $\ell$ (let's assume it does not contain $A$).
How can we find points $B$ and $C$ such that $\{B,C\} = \mathcal E \cap \ell \neq \emptyset$ using straight edge and compass?
We can easily get:
- center of $\mathcal E$ as it is the midpoint of $F_1F_2$
- axes of symetry of $\mathcal E$
- major axis:
$X = \odot(A,AF_1) \cap \overleftrightarrow{AF_2}$ (with $X$ and $F_2$ in disjointed halfplanes of $AF_1$).
if $M$ is the midpoint of $XF_2$, then $a = F_2M$ so we have the vertices of the ellipse.