Clairaut differential equations and elliptic discriminants

Question

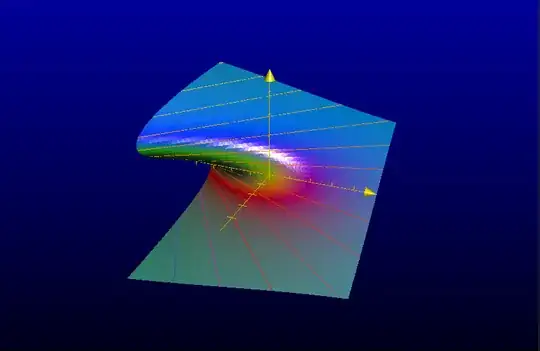
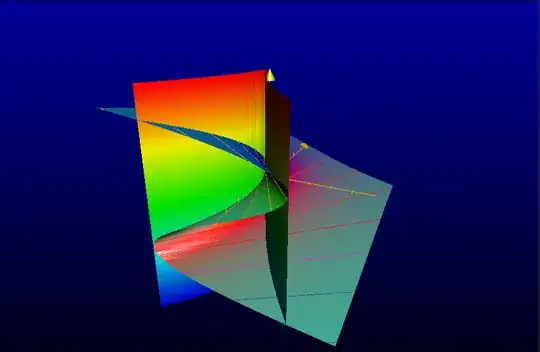
I was solving this math.SE question, which was asking to solve the Clairaut differential equation $y= xy' - (y')^3$. Just to have nicer signs, I then looked at the equivalent equation $$ y= xy' + (y')^3 .$$ The main trajectories of this differential equation are:

• the algebraic curve given by $27y^2 + 4x^3 = 0$;
• all the lines tangent to this curve.

Many of us have already seen this curve somewhere: in fact, the discriminant of the elliptic curve (in Weierstrass form) $$ y^2 = x^3 +ax+b $$ is $$ \Delta = 4a^3+27b^2.$$

My question is:

What is the relation between this Clairaut's differential equation and the discriminant of elliptic curves in Weierstrass form?

In other words, I ask if this is just a coincidence, or there is indeed some natural construction that relates the two.

---

On one hand, it is easy to verify that the Clairaut equation is satisfied by the discriminant. It should be easy to verify this without using the discriminant formula, in this fashion:

"Suppose that an elliptic Weierstrass equation with parameters $(a,b)$ is singular (this is a reformulation of $\Delta =0$); then if we move the parameters in a curvy special direction, dictated by the Clairaut differential equation, then the cubic Weierstrass curve remains singular."

This approach is a bit sketchy, because actually also the tangent lines to the zero-discriminant locus are solutions. Then, I guess that one should study what happens to the Weierstrass curve when the parameters move along these lines, and identify some "quasi-invariant" or "property" along these lines. This property should be, in some sense, some kind of generalization of the property "the weierstrass curve is singular". Then the Clairaut differential equation should be a differential equation valid "along these quasi-invariants".

For completeness, here is the general equation of the tangent lines to the curve $4x^3+27y^2=0$: $$y = mx+m^3,$$ where $m$ is some parameter.

---

As a follow-up, it would be great if there were some relationship between Clairaut differential equations (or some other class of differential equations) and discriminants of families of algebraic cuves (or better, these "generalized discriminants" that include somehow the lines tangents to the "zero-discriminant locus"). But this would be perhaps a separate question.

Answer 1

Firstly, let's introduce a function $F(x,y,p) = p^3 + px - y$, where $p$ is our substitution for $y'$. Here is a picture of the surface $F(x,y,p) = 0$.

There is a field of tangent plains on $F(x,y,p) = 0$: $$ dF = 0 \Leftrightarrow (3 p^2 + x)dp + p dx - dy = 0. $$ It is defined everywhere, but we are only interested in its restriction to our surface.

There is another important field here, the field of contact planes. It is defined as $$ p dx - dy = 0 $$ and represents the condition $y' = p$.

The original equation is closely related to the following system of equations: $$ \left\{\begin{aligned} &F(x,y,p) = p^3 + px - y = 0 \\ &dF(x,y,p) = (3 p^2 + x)dp + p dx - dy = 0\\ &p dx - dy = 0 \end{aligned}\right. . $$

The first equations defines the surface where the original equation feels itself at home. The second one defines tangent planes, and the third one is the definition of $p$. The intersections of tangent planes with contact planes define a slope field on the surface, i.e. a differential equation. This equation has integral curves (the lines on the picture). To obtain integral curves of the original equation, we just need to project the curves on the surface onto the plane $xy$.

But there're some subtle moments. And the most important one is those points on the surface, where the tangent plane and the contact plane coincides. Those points are bad even for the equation on the surface: a solution exists, but it is not unique.

In our particular case, this happens when $3 p^2 + x = 0$ (exactly when tangent planes are vertical). To make some conclusions, we have to combine this equality with the first equation: $$ y = p^3 + px \Rightarrow 27 y^2 = (3p^2)^3 + 6x(3p^2)^2 + 9x^2(3p^2) \Rightarrow 27y^2 = (-x)^3 + 6x(-x)^2 + 9x^2(-x), $$ so we get $$ 27 y^2 + 4x^3 = 0. $$ This curve is called the discriminant curve :) By the construction, all good solutions, intersecting this curve, are tangent to it.

As we can see in the picture above, it is indeed the discriminant curve in the algebraic sense: singularities of the differential equation coincide with those points, where two solutions merge with each other.

General case:

In general, we have the following equations:

$$ y = px + f(p) \Leftrightarrow \left\{\begin{aligned} &F(x,y,p) = f(p) + px - y = 0 \\ &dF(x,y,p) = (f'(p) + x)dp + p dx - dy = 0\\ &p dx - dy = 0 \end{aligned}\right. . $$

There's one feature of the Clairaut equation: critical points of the surface, where the tangent plane is vertical, $f'(p) + x = 0$, coincide with points, where the contact plane is tangent to the surface.

We can easily get all integral curves. Subtracting the third equation from the second one, we get: $$ \left\{\begin{aligned} &y = px + f(p) \\ &(f'(p) + x)dp = 0 \end{aligned}\right. . $$ Therefore, except for critical points, $p = \mathrm{const} = C$ along the solutions. Hence projections of integral curves onto $xy$ are lines $u = Cx + f(C)$.

The discriminant curve can be found from $$ \left\{\begin{aligned} &y = px + f(p) \\ &f'(p) + x = 0 \end{aligned}\right. . $$

As we can see, for each $C \in \mathbb R$ $y = Cx + f(C)$ and the discriminant curve has a common point $P_C = \left(- f'(C), -C f'(C) + f(C)\right)$. By the construction of the discriminant curve, $y = Cx + f(C)$ is tangent to the curve at $P_C$. Moreover, each point on the curve corresponds to some solution of the form $y = Cx + f(C)$, because those solutions are intersections of planes $p = \mathrm{const}$ with the surface.

Fact: Strictly concave function $f$, which defines the Clairaut equation $y = px - f(p)$, is the Legendre transform of a function $g$, which defines the envelope of the solutions by $y = g(x)$.

However, $f(p) = p^3$ doesn't meet the requirement. Fortunately, there's a more general notion of projective duality. In the general case, $f$ and the discriminant curve are projectively dual to each other, since each solution of the form $y = Cx + f(C)$ is tangent to the curve, and each point of the curve has a tangent line corresponding to some solution.

I hope I was able to give you some good insight. If you'll have any questions, feel free to ask :)