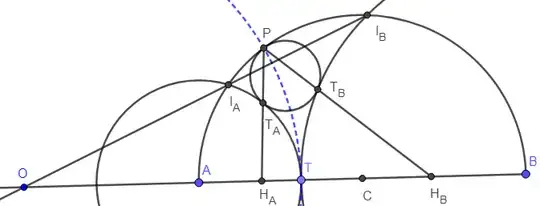
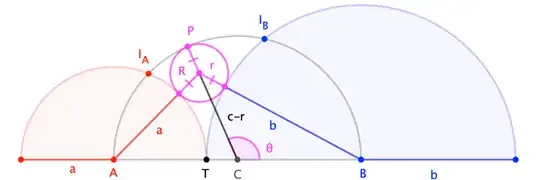
Let (semi-)circles $\bigcirc A$, $\bigcirc B$, $\bigcirc C$ have radii $a$, $b$, $c:=\frac12(a+b)$, and suppose $\bigcirc R$ of radius $r$ is externally tangent to $\bigcirc A$ and $\bigcirc B$, and internally tangent to $\bigcirc C$ at $P$. (It shouldn't matter, but in case of sign error, I'm assuming $b>a$, as in the figure.)
(I'll note that the lines from $P$ through the other points of tangency necessarily meet $\overline{AB}$ at OP's centers of in-similitude $H_A$ and $H_B$. This is a property of the configuration, not a constraint, so we'll ignore it.)
Now, as $\overline{CR}$ is a median of $\triangle ARB$, Apollonius gives us this relation:
$$\begin{align}
|AR|^2+|BR|^2=2(|CR|^2+|AC|^2) &\quad\to\quad (a+r)^2+(b+r)^2=2((c-r)^2+c^2 ) \\[4pt]
&\quad\to\quad r = \frac{a b}{2(a+b)} \tag1
\end{align}$$
If we coordinatize, with $C=(0,0)$, $A=(-c,0)$, $B=(c,0)$, we can write $P= (c\cos\theta, c\sin\theta)$, where $\theta := \angle BCP$. The Law of Cosines in $\triangle CBR$ gives us
$$\cos\theta = \frac{-|BR|^2+|CB|^2+|CR|^2}{2|CB||CR|}=\frac{-(b+r)^2+c^2+(c-r)^2}{2c(c-r)}=\frac{(a-b)((a+b)^2+ab)}{(a+b)((a+b)^2-ab)} \tag2$$
Let the perpendicular bisector of $\overline{PT}$ meet $\overleftrightarrow{AB}$ at $Q'$ (which is therefore the center of a circle through $P$ and $T$). Using coordinates, we obtain
$$|Q'C|=\frac{a^2 + a b + b^2}{2\,|a-b|} \tag{3}$$
Shifting focus to the points $I_A$ and $I_B$ where $\bigcirc A$ and $\bigcirc B$ meet $\bigcirc C$, we can calculate
$$I_A = \left(\frac{a^2-2ab-b^2}{2(a+b)},\frac{av}{a+b}\right) \qquad I_B=\left(\frac{a^2+2ab-b^2}{2(a+b)},\frac{bu}{a+b}\right) \tag{4}$$
where
$$u := \sqrt{a(a+2b)}\qquad v := \sqrt{b(b+2a)}$$
Let $\overleftrightarrow{I_AI_B}$ meet $\overleftrightarrow{AB}$ at $Q$. (This corresponds to the definition of OP's point $O$.) We find that
$$|QC|=\left|\frac{a v (a^2 + 2 a b - b^2) -
b u (a^2 - 2 a b - b^2)}{2 (a + b) (a v - b u)}\right|=\frac{(a u + b v)^2}{2 (a + b)^2 |a - b|} \tag{5}$$
Since $(5)$ and $(3)$ do not match (unless $a=b$, a case we can ignore), we conclude that $Q$ and $Q'$ are distinct points.

This says that OP's point $O$ is not the center of a circle through $T$ and $P$; the "magic" is an illusion. $\square$
It's a pretty good illusion, though. One can calculate the discrepancy relative to the diameter of $\bigcirc C$ as
$$\frac{|QQ'|}{|AB|} = \frac{a b (u - v)^2}{2 (a + b)^3 |a - b|} \tag{6}$$
For, say, $(a,b)=(3,5)$, this gives $|QQ'|/|AB|\approx 0.0100$. Further, one can show
$$|QT|=\frac{a b (a^2 + a b + b^2 + u v)}{ (a + b)^2|a - b|} \qquad |QP|=\frac{u v (a u + b v) \sqrt{a b}}{ (a + b)^2|a - b| \sqrt{a^2 + a b + b^2}} \tag{7}$$
For $(a,b)=(3,5)$, the relative discrepancy in these values is
$$\frac{\left|\;|QP|-|QT|\;\right|}{|AB|}= 0.000550\ldots$$
which is easy to miss, visually. I was almost convinced of the "magic" myself, but moving my GeoGebra sketch to make $a$ and $b$ dramatically different revealed how things didn't quite match up.