A tough integral $\int_0^{\infty}\frac{\operatorname{sech}(\pi x)}{1+4x^2}\, \mathrm dx $

Question

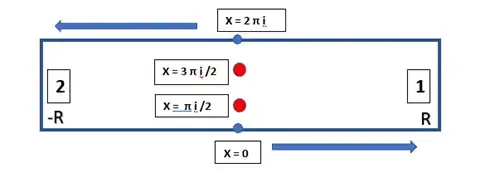
I was working on an integral which I found on Quora. I simplified it a lot and ended up with this intgeral

$$\int_0^{\infty}\dfrac{\operatorname{sech}(\pi x)}{1+4x^2}\, \mathrm dx $$

I tried converting this into exponential form and using geometric series which ended up in this.

$$2\sum_{k=0}^\infty (-1)^k\int_0^\infty \dfrac{e^{-(2k+1)\pi x}}{4x^2+1}\, \mathrm dx $$

I didn't try to solve this using exponential integral, as I am not that much familiar with it.

Using Wolfram|Alpha, I figured out that this integral is equal to $\frac{1}{2}\ln{2}$. The simple answer makes me suspect if the integral is just a tricky one.

How can I evaluate this integral, using this method or any other method, except contour integration?

Answer 1

Integrate as follows

\begin{align} &\int_0^{\infty}\frac{\operatorname{sech}(\pi x)}{1+4x^2}\>dx\\ \overset{t=2\pi x }=& \frac\pi2 \int_{-\infty}^{\infty}\frac{e^{\frac t2}}{(e^t+1)(\pi^2+t^2)}dt\\ =& \frac\pi2 \int_{-\infty}^{\infty}\frac{e^{\frac t2}}{e^t+1}Re\left(\frac1\pi \int_0^\infty e^{-(\pi-i t)y }dy\right)dt\\ =& \frac12 Re\int_{0}^{\infty}e^{-\pi y} \left(\int_{-\infty}^\infty \frac{e^{a t}}{e^t+1}dt \right)dy \>\>\>\>\>\>\>a= iy+\frac12\\ \overset{x=e^t}=& \frac12 Re\int_{0}^{\infty}e^{-\pi y} \left(\int_{0}^\infty \frac{x^{a-1}}{x+1}dx \right)dy \\ =& \frac12Re \int_{0}^{\infty}e^{-\pi y}\pi\csc(\pi a)\,dy \\ =& \int_{0}^{\infty} \frac\pi{e^{2\pi y}+1}dy \overset{t=e^{-2\pi y}}=\frac12\int_0^1 \frac1{1+t}dt\\ =&\frac12\ln2 \end{align}

Answer 2

All proposed different ways of solution to the problem are really nice. In my opinion, contour integration "catches" the symmetry of this problem deeper and allows to get the closed answer to more general problem.

Let's denote $$I(a)=\int_{-\infty}^\infty\frac{dx}{(e^{\pi x}+e^{-\pi x})(a^2+x^2)}$$ Then $$I_0=\int_0^{\infty}\dfrac{\operatorname{sech}(\pi x)}{1+4x^2}\, \mathrm dx=\frac{1}{4}\int_{-\infty}^\infty\frac{dx}{(e^{\pi x}+e^{-\pi x})(\bigl(\frac{1}{2}\bigr)^2+x^2)}=\frac{1}{4}I\Bigl(\frac{1}{2}\Bigr)$$ Let's also consider $$J(a)=\int_{-\infty}^\infty\frac{\log\bigl(a^2+x^2\bigr)}{e^{\pi x}+e^{-\pi x}}dx$$

Then $I(a)=\frac{1}{2a}\frac{\partial}{\partial a}J(a)$ and

$$J(a)=2\,\Re\int_{-\infty}^\infty\frac{\log\bigl(a-ix\bigr)}{e^{\pi x}+e^{-\pi x}}dx=\frac{2}{\pi}\Re\int_{-\infty}^\infty\frac{\log\bigl(a-\frac{it}{\pi}\bigr)}{e^t+e^{-t}}dt$$ $$=\frac{2}{\pi}\Re\int_{-\infty}^\infty\frac{\log\bigl(\frac{a}{2}-\frac{it}{2\pi}\bigr)+\log2}{e^t+e^{-t}}dt=J_1(a)+J_2$$ where $$J_2=\frac{2\log2}{\pi}\int_{-\infty}^\infty\frac{dt}{e^t+e^{-t}}=\frac{2\log2}{\pi}\int_{-\infty}^\infty\frac{e^tdt}{e^{2t}+1}=\frac{2\log2}{\pi}\int_{0}^\infty\frac{dx}{x^2+1}=\log2$$ To evaluate $J_1(a)$ we follow the approach developed by Iaroslav V. Blagouchine (here)

Noting that $\log z=\log\Gamma (z+1)-\log\Gamma(z)$ $$J_1(a)=\frac{2}{\pi}\Re\int_{-\infty}^\infty\frac{\log\bigl(\frac{a}{2}-\frac{it}{2\pi}\bigr)}{e^t+e^{-t}}dt=\frac{2}{\pi}\Re\int_{-\infty}^\infty\frac{\log\Gamma\bigl(\frac{a}{2}-\frac{it}{2\pi}+1\bigr)-\log\Gamma\bigl(\frac{a}{2}-\frac{it}{2\pi}\bigr)}{e^t+e^{-t}}dt$$

Next, we choose a rectangular contour C in the complex plane

Noting that integral along the path $(1)$ and $(2)$ wanish as $R\to\infty$ and that $e^{2\pi i+t}=e^t$, we can write: $$J_1(a)=-\frac{2}{\pi}\Re\oint_C\frac{\log\Gamma\bigl(\frac{a}{2}-\frac{iz}{2\pi}\bigr)}{e^z+e^{-z}}dz=\Re\biggl(-2\pi i \frac{2}{\pi}\operatorname*{Res}_{\binom{z=\pi i/2}{z=3\pi i/2}}\frac{\log\Gamma\bigl(\frac{a}{2}-\frac{iz}{2\pi}\bigr)}{e^z+e^{-z}}\biggr)=2\Bigl(\log\Gamma\bigl(\frac{a}{2}+\frac{3}{4}\bigr)-\log\Gamma\bigl(\frac{a}{2}+\frac{1}{4}\bigr)\Bigr)$$ $$J(a)=\int_{-\infty}^\infty\frac{\log\bigl(a^2+x^2\bigr)}{e^{\pi x}+e^{-\pi x}}dx=J_1(a)+J_2=2\Bigl(\log\Gamma\bigl(\frac{a}{2}+\frac{3}{4}\bigr)-\log\Gamma\bigl(\frac{a}{2}+\frac{1}{4}\bigr)\Bigr)+\log2$$ Taking derivative with respect to $a$ we can easily evaluate expressions like $\int_{-\infty}^\infty\frac{dx}{(e^{\pi x}+e^{-\pi x})(a^2+x^2)^n}$.

For example, $$I_0=\int_0^{\infty}\dfrac{\operatorname{sech}(\pi x)}{1+4x^2}\, \mathrm dx=\frac{1}{4}I\bigl(a=\frac{1}{2}\bigr)=\frac{1}{4}\frac{1}{2a}\frac{\partial}{\partial a}J(a)|_{a=1/2}=\frac{1}{8a}\Bigl(\Psi\bigl(\frac{a}{2}+\frac{3}{4}\bigr)-\Psi\bigl(\frac{a}{2}+\frac{1}{4}\bigr)\Bigr)|_{a=1/2}$$ $$I_0=\frac{1}{4}\Bigl(\Psi(1)-\Psi(\frac{1}{2})\Bigr)=\frac{\log2}{2}$$ where $\Psi(x)=\frac{\partial}{\partial x}\log\Gamma(x)$ - digamma function.

Answer 3

The question asks for anything "except contour integration", but actually the latter is the very first thing I would apply here. So this answer follows the contour integration approach for reference.

The integral is $\frac12\int_{-\infty}^\infty$, so that if $I_{R,N}=\int_{C_{R,N}}\frac{\operatorname{sech}\pi z}{1+4z^2}\,dz$ where, for $R>0$ and $N$ a positive integer, we take $C_{R,N}$ to be the boundary of $[-R,R]+i[0,N]$, then $\lim\limits_{R\to\infty}\lim\limits_{N\to\infty}I_{R,N}$ is twice the given integral, and it equals $2\pi i$ times the sum of the residues of the integrand at $z=i(n+1/2)$ over $n\in\mathbb{Z}_{\geqslant 0}$ ($n=0$ is a double pole, $n>0$ are simple poles): $$\operatorname*{Res}_{z=i/2}\frac{\operatorname{sech}\pi z}{1+4z^2}=\frac1{4\pi i},\quad\operatorname*{Res}_{z=i(n+1/2)}\frac{\operatorname{sech}\pi z}{1+4z^2}=\frac1{4\pi i}\frac{(-1)^{n-1}}{n(n+1)}.\quad(n>0)$$ Hence the value of the given integral is, as conjectured, $$\frac14\left[1+\sum_{n=1}^\infty(-1)^{n-1}\left(\frac1n-\frac1{n+1}\right)\right]=\frac14\big(1+\ln2-(1-\ln2)\big)=\frac{\ln2}{2}.$$

Answer 4

A short solution by using the series of $\operatorname{sech}(x)$.

Since $$\operatorname{sech}(x)= 4\sum_{k=0}^{\infty}\frac{(-1)^k(2k+1)\pi}{(2k+1)^2\pi^2+4x^2}$$ and then we have $$\int_0^{\infty}\frac{\operatorname{sech}(\pi x)}{1+4x^2}dx=\frac{4}{\pi}\sum_{k=0}^{\infty}{(-1)^k(2k+1)}\int_0^{\infty}\frac{dx}{(m^2+4x^2)(1+4x^2)}=$$ where $m=2k+1$ and by partial fraction decomposition we easily can deduce the integral $$\int_0^{\infty}\frac{dx}{(m^2+4x^2)(1+4x^2)}=\frac{\pi}{4m(m+1)}=\frac{\pi}{4(2k+1)(2k+2)}$$ and hence we have $$\sum_{k=0}^{\infty}\frac{(-1)^k}{2(k+1)}=\frac{1}{2}\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k}=\frac{\log(2)}{2}$$

Answer 5

Note that your integrand is even in $x$, so that you are really concerned with

$$ \frac{1}{2}\int_{\mathbb{R}} \operatorname{sech}(\pi x) \frac{1}{1+4x^2}\,dx.$$

If you're willing to accept Fourier transform techniques, we have

$$ \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}} e^{-ixy}\operatorname{sech}(\pi x)\,dx = \frac{1}{\sqrt{2\pi}}\operatorname{sech}\bigg(\frac{y}{2}\bigg) $$

and also

$$ \frac{1}{\sqrt{2\pi}} \int_{\mathbb{R}} e^{-ixy} \frac{1}{1+4x^2}\,dx = \frac{1}{2}\sqrt{\frac{\pi}{2}} e^{-|y|/2}. $$

Then from Parseval's theorem,

\begin{align} \frac{1}{2}\int_{\mathbb{R}} \operatorname{sech}(\pi x) \frac{1}{1+4x^2}\,dx &= \frac{1}{2} \int_{\mathbb{R}} \frac{1}{\sqrt{2\pi}} \operatorname{sech}\bigg(\frac{y}{2}\bigg) \frac{1}{2}\sqrt{\frac{\pi}{2}} e^{-|y|/2}\,dy \\ &= \frac{1}{4} \int_0^{\infty} \operatorname{sech}\bigg(\frac{y}{2}\bigg) e^{-y/2}\,dy. \end{align}

As for this integral, note that $\operatorname{sech}(x) = \frac{2}{e^x + e^{-x}}$ so that we are left to evaluate

$$ \frac{1}{2}\int_0^{\infty} \frac{e^{-y/2}}{e^{y/2} + e^{-y/2}}\,dy. $$

Let $z = e^{-y/2}$, then $dz = -\frac{1}{2} e^{-y/2}\,dy$, to give

$$ \int_0^1 \frac{1}{z^{-1}+z}\,dz = \int_0^1 \frac{z}{1+z^2}\,dz = \frac{\log(2)}{2}.$$