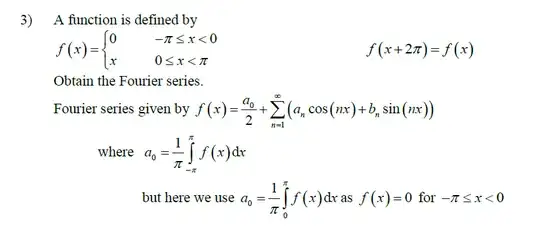For example: I need to do a Fourier Transform on f(t)*h(t), h(t) is 1 for t>0 and 0 for t <0, the answers for several questions end up using the usual formula but integrate from 0 to infinity which is fine, however should we not divide by 2 to account for the -infinity to 0 part of the function?
I have done many similar questions recently in learning the Fourier Series and when simplifying the integral in a similar fashion, we ALWAYS divided by two.