Why does this diagram not commute?

Question

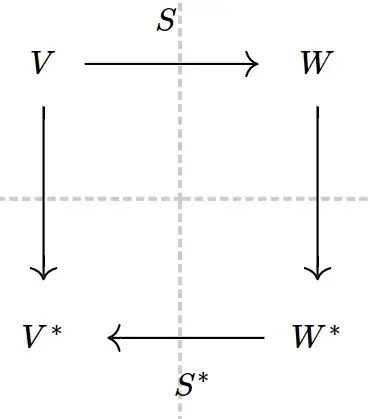
When I look at the following commutative Diagram involving two vector spaces and the linear map $S$, why does it not seem to commute? Should it even commute?

For example if $\text{dim} V = 2$ und $\text{dim} W = 1$, then the rank of $S^* = 1$ but rank of the map to its dual space could be $2$. This somehow confuses me, why does it behave that way?

before even speaking of the diagram commuting, you have to define the maps. What are the maps $V\to V^$ and $W\to W^$? — peek-a-boo, Jun 17 '21 at 20:49
What choice did you make for the maps from the spaces to their duals? — Anthony, Jun 17 '21 at 21:17
@Andreas Blass, yes, that's right. I meant the map onto its dual space. — TheFibonacciEffect, Jun 18 '21 at 05:13
@Anthony Saint-Criq I learned there is a Functor between any vector space and it's dual, that also maps every map/arrow in the category of vector spaces to its dual. But that doesn't really describe the map itself, does it? In the finite dimensional case I would consider the map implied by Riesz, I don't know about the infinite dimensional case. However as subrosar pointed out there is no canonical way to do this. — TheFibonacciEffect, Jun 18 '21 at 05:16

score 5 · Accepted Answer · answered Jun 17 '21 at 21:14

I am understanding your question as asking about vector spaces $V,W$, their duals $V^*$ and $W^*,$ a linear map $S$ and its dual $S^*$ and given isomorphisms from $V$ to $V^*$ and $W$ to $W^*.$ In general, this diagram is not expected to commute. This noncommutativity is related to the fact that it is generally impossible to choose a canonical isomorphism from a vector space to its dual. That is to say that isomorphisms from $V$ to $V^*$ and $W^*$ cannot be chosen in a unique way and will likely have nothing to do with each other. The situation is different if we are considering canonical isomorphisms from two vector spaces to their double dual. See, for example, Motivation to understand double dual space.

score 4 · Answer 2 · answered Jun 17 '21 at 21:53

Yes, it is fairly surprising that no broad version of such a family of diagrams can commute.

Even if we restrict out attention to finite-dimensional Hilbert spaces over $\mathbb R$, and use the Riesz-Fischer isomorphism of $V$ to $V^*$, the analogous diagram does not commute unless $S$ is an isometry to its image. This is already clear with two-dimensional real Hilbert spaces.

For emphasis: it did surprise me considerably some years ago when I came to understand that the Riesz-Fischer isomorphism is generally "not functorial" ... in the sense that the expected diagram fails to commute. For me, this arose in looking at things like $H^1\to L^2\to H^{-1}$ where $H^i$ are Sobolev spaces, and $H^{-1}$ is dual to $H^1$... Details about this would probably be too tangential to the basic question here.

Why does this diagram not commute?

2 Answers2