natural exact triple sequence, Mayer-Vietoris sequence

Question

I have some questions on the proof of the following lemma, which is used to deduce the exactness of triple sequences, of the rows in the Mayer-Vietoris sequence.

Let $(\mathcal{H}_\ast, \partial_\ast)$ be a homology theory.

Lemma:

Let $(X,B,A)$ be a triple, hence $X$ is a topological space and $A\subseteq B\subseteq X$. Then it exists a natural exact triple sequence:

$\dotso\stackrel{\partial_{n+1}(X,B,A)}{\longrightarrow}\mathcal{H}_{n}(B,A)\stackrel{\mathcal{H}_{n}(i)}{\longrightarrow}\mathcal{H}_{n}(X,A)\stackrel{\mathcal{H}_{n}(j)}{\longrightarrow}\mathcal{H}_n(X,B)\\ \dotso\stackrel{\partial_{n}(X,B,A)}{\longrightarrow}\mathcal{H}_{n-1}(B,A)\stackrel{\mathcal{H}_{n-1}(i)}{\longrightarrow}\mathcal{H}_{n-1}(X,A)\stackrel{\mathcal{H}_{n-1}(j)}{\longrightarrow}\mathcal{H}_{n-1}(X,B)$

where $i:(B,A)\to (X,A)$ and $j: (X,A)\to (X,B)$ are the inclusions.

Proof:

Define the connecting homomorphism

$\partial_n(X,B,A):\mathcal{H}_n(X,B)\stackrel{\partial_n(X,B)}{\longrightarrow}\mathcal{H}_{n-1}(B)\stackrel{\mathcal{H}_{n-1}(k)}{\longrightarrow}\mathcal{H}_{n-1}(B,A)$, where

$k: B\to (B,A)$ is the inclusion.

The composition $\mathcal{H}_n(B,A)\to\mathcal{H}_n(X,A)\to\mathcal{H}_n(X,B)$ is the null morphism, since we can write it as the composition $\mathcal{H}_n(B,A)\to\mathcal{H}_n(B,B)\to\mathcal{H}_n(X,B)$ and $\mathcal{H}_n(B,B)=0$ by the long exact sequence of the pair $(B,B)$.

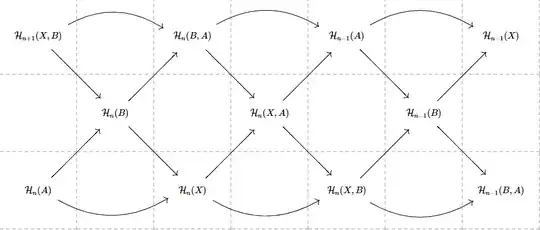
The exactness of the long exact sequence of pairs $(X,B), (X,A)$ and $(B,A)$ and a diagram chase in the braid:

gives the exactness of triple sequences. The naturality of $\partial_n(X,B,A)$ follows from the naturality of $\partial_n(X,B)$.

---

I have some questions regarding this proof, as I am new to homology theory.

1.

The composition $\mathcal{H}_n(B,A)\to\mathcal{H}_n(X,A)\to\mathcal{H}_n(X,B)$ is the null morphism, since we can write it as the composition $\mathcal{H}_n(B,A)\to\mathcal{H}_n(B,B)\to\mathcal{H}_n(X,B)$

Why can we do this? Is it because the inclusion $i: (B,A)\to (X,A)$ maps the pair $(B,A)$ onto $(B,A)$, and we can just write this as $(B,B)$ as $A\subseteq B$. Or do I need the axiom of homotopy invariance here?

2.

$\mathcal{H}_n(B,B)=0$ by the long exact sequence of the pair $(B,B)$.

From the long exact sequence we get that the image of

$\mathcal{H}_n(i):\mathcal{H}_n(B)\to\mathcal{H}_n(B)$ is the kernel of

$\mathcal{H}_n(j):\mathcal{H}_n(B)\to\mathcal{H}_n(B,B)$.

So when I can show that $\ker(\mathcal{H}_n(i))=\{0\}$ I am done. So why is $\mathcal{H}_n(i)$ injective? This follows because the inclusion is of course injective.

Then $i$ has for instance right inverse $r$, and from the functorial property we would see that $\mathcal{H}_n(i)\circ\mathcal{H}_n(r)=\mathrm{id}$, so $\mathcal{H}_n(i)$ is also injective.

Then the image of $\mathcal{H}_n(j)$ is $\{0\}$, so $\mathcal{H}_n(B,B)=0$.

Would this be correct?

3.

The exactness of the long exact sequence of pairs $(X,B), (X,A)$ and $(B,A)$ and a diagram chase in the braid: [...] gives the exactness of triple sequences.

How would a diagram chase look like to prove the exactness? Can you give an example? This looks tedious to prove that this sequence is exact.

4.

The naturality of $\partial_n(X,B,A)$ follows from the naturality of $\partial_n(X,B)$.

TODO... (I think this is easy, but I will think about it later)

Answer 1

1. The composition of the inclusions $(B,A)\subset(X,A)\subset(X,B)$ is the inclusion map $(B,A)\to(X,B)$, so by functoriality the same is true of the induced maps on homology. The same statement holds if we replace $(X,A)$ by $(B,B)$. The composition thus factors through $H_n(B,B)$.

2. The inclusion map $B\to B$ is the identity map, so it induces the identity map – an isomorphism – on homology.

Answer 2

To (partly) address question 3, diagram chases are tedious, which is why they got named and are so often omitted --- they tend to follow a pattern, but it's a long and slow one.

If you want an example of this, I recommend Vick's Homology Theory (https://www.amazon.com/Homology-Theory-Introduction-Algebraic-Mathematics/dp/1461269334), which has, perhaps in its proof of the five-lemma?, at least one rather long and detailed diagram-chase; once you've seen and followed that, you'll have a good idea of how all other diagram chases look.

I don't assert that Vick is the best source --- just a source that I know has a diagram chase worked out in detail, because it's where I first saw one.