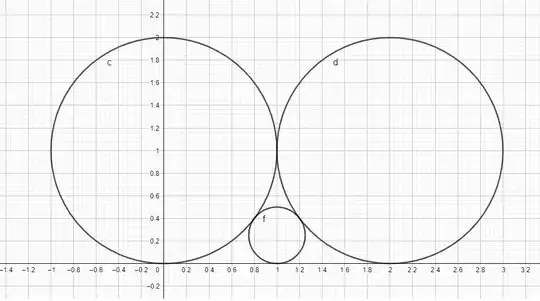
Let these circles with radiuses $r1, r2, r3,$ and $r3$ is the smallest radius. Also let the following operator $*$ be defined as $$x * y = \frac{xy}{(x^{\frac{1}{2}} + y^{\frac{1}{2}})^2}$$
then it can be proven that $r3 = r1 * r2, \forall r1, r2 \in [0, \infty)$.
It can also be proven that $x * x * x \ * \ ... \ * \ x = \frac{x}{n^2}$ when $n$ is the number of times $x$ has been composed $\forall n \in \mathbb{N} - \{0\}$.
Let $x \circ y = \pi (x * y)(x * y) + x \circ (x * y) + y \circ (x * y)$.
$x \circ y \ $ will equal an infinite sum of circle areas that are between the two starting circles with radii equal to $x$ respectively $y$.
I want to find out towards what value $x \circ y$ converges.
It can also be reasoned that $x \circ y = \binom{n + m}{n} (\frac{x}{n^2} * \frac{y}{m^2})$ where $(n, m)$ takes all pairs of ordered integers.