Given $G=(V,E)$, let $\mathbb{R}^V$ be the set of all real vectors $x=(x_v)_{v\in V}$ where each component $x_v$ corresponds to a vertex $v\in V$. Let $Q_G$ be defined $$Q_G:=\{x\in\mathbb{R}^V\;|\;x_u+x_v\geq1\text{ for all }\{u,v\}\in E\text{ and } x_v\geq0\text{ for all }v\in V\}$$
My Thinking
We know that if we can show that the matrix $A$ representing the constraints of our graph, is totally unimodular, then all vertices in $Q_G$ are integral.
Let's consider a simple graph (The picture below also includes the criteria for being totally unimodular)
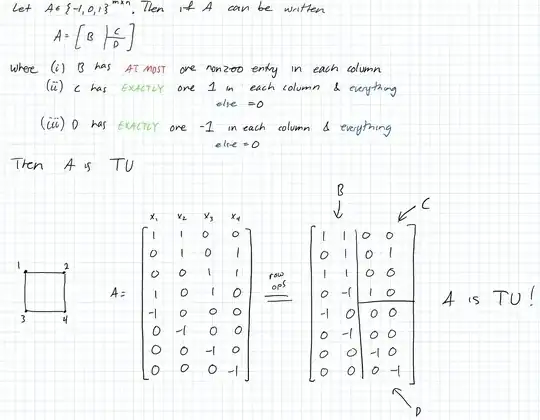
In this simple example, we can see that it the statement we are trying to prove is true. But I am having trouble coming up with a formal proof for this.
Edit
I made a mistake on satisfying the criteria for (i). But we can always use row operations to get rid of the extra non-zero values in $B$ so it still holds that $A$ is totally unimodular. For example, adding rows 5 and 6 to rows 1,2, and 3 appropriately will allow us to satisfy the criteria for $B$ without messing with $C$ or $D$.