I'm studying Sharp's Steps in Commutative Algebra, and I need a hint how to proceed with this exercise in the page 26:
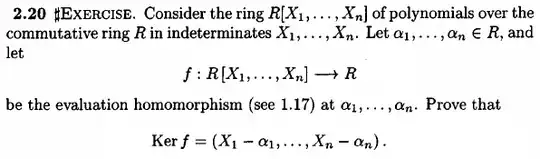
First of all, I didn't understand even the notation, what did the author mean by $(X_1-\alpha_1,...,X_n-\alpha_n)$?
Thanks a lot.
I'm studying Sharp's Steps in Commutative Algebra, and I need a hint how to proceed with this exercise in the page 26:
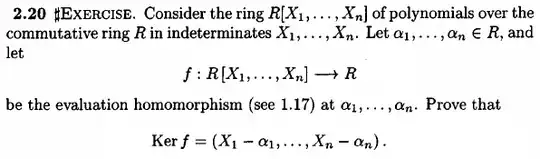
First of all, I didn't understand even the notation, what did the author mean by $(X_1-\alpha_1,...,X_n-\alpha_n)$?
Thanks a lot.
Hint: by the division algorithm, $\, g = (x_1\! -\! a_1) q_1 + r_1,\ $ for $\ r_1\in R[x_2,\ldots,x_n].\,$ By induction, $\,r_1 = (x_2\!-\!a_2)q_2 +\cdots + (x_n\!-\!a_n)q_n + r_n,\,$ for $\,r_n\in R.\ $ Evaluating at $\,x_i = a_i\,$ yields $\,g(a_i) = 0\iff r_n = 0\iff g\in (x_1\!-\!a_1,\ldots,x_n\!-\!a_n)$
Basically the problem can be translated as "Show that if a polynomial in $n$ variables has $(\alpha_1,\ldots,\alpha_n)$ as a root, then it is of the form $f_1\cdot(x_1-\alpha_1)+\ldots +f_n\cdot (x_n-\alpha_n)$ for some polynomials $f_1,\ldots,f_n$.
Can you do this for a polynomial in 1 or 2 variables?