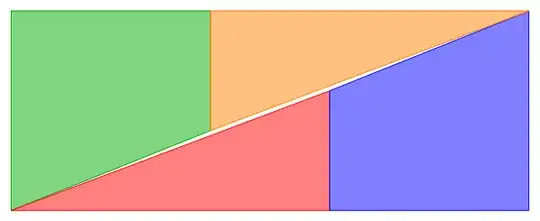
In the attached image i have shown a square whose area comes out as 64. Now that square is cutted to make a rectangle and the area of rectangle comes out as 65. How is it possible when same material is their and no more material is added ? Thanks for your time .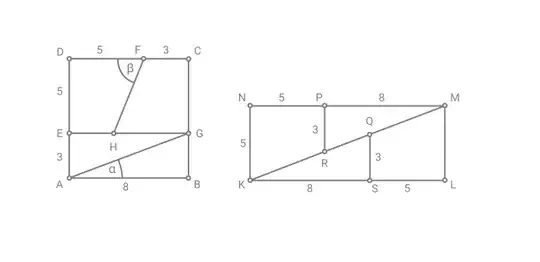
Asked
Active
Viewed 265 times
1
Weronika
- 554
3 Answers
3
This is happening because the "rectangle" you have formed isn't a prefect rectangle. Notice that, if $\angle MKL=\theta$, then, for a perfect triangle, we would have $$\tan \theta=\frac {QS}{SK}=\frac {ML}{LK}$$ But here you can clearly see that: $$\frac 38\neq \frac {5}{13}$$ Hence $MKL$ is not a triangle and the figure formed is not a rectangle.
Ritam_Dasgupta
- 6,052
2
The points $K$, $R$ and $Q$ (or really any three points from $\{K,R,Q,M\}$) aren't aligned. If $K=(0,0)$, then $R=(5,2)$ and $Q=(8,3)$. Therefore $K$ and $R$ lie on the line $2x-5y=0$ and $K$ and $Q$ lie on the line $3x-8y=0$. The quadrilateral $KRMQ$ provides the remaining area of $1$.
For the record, there are a few non-equivalent ways to read the diagram on the right. Mine, of course, is under the assumption that $M,P,N$ are aligned, that $K,S,L$ are aligned and that both $MN$ and $KL$ are perpendicular to $KN$. We could also give different interpretations where, instead, all the points that look colinear are colinear, but the angles are tweaked. Fortunately people aren't quite as eager to inspect which areas become different in these cases, because their scarce interest in highly irregular quadrilaterals (which we share) quickly outweighs their urge to find paradoxes.
