4

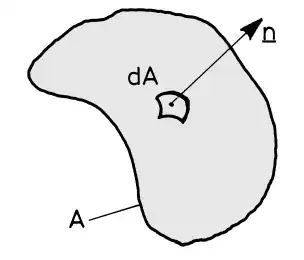
I consider a closed area $ A $ and a piece of area $dA$ from it. Now let be $ \underline{n} $ the normal vector of $ dA $. Then we call $ d\underline{A}:=\underline{n}\cdot dA $ the area vector.

enter image description here

Now here are my problems:

1.) I don't see why $ \oint d\underline{A}=\underline{0} $.

2.) I struggle with this weird notation just writing the symbol $ d\underline{A} $ into to this integral. I'm used to use this notation like this for example $ \int f(x)\space dx $.

3.) Is there some (physical) interpretation for the integral $ \oint d\underline{A} $ ?

Bernard
  • 179,256
hallo007
  • 580
  • Who says $\oint d\underline{A}=\underline{0}$? Exactly what did they say? – David K Apr 28 '21 at 16:43
  • It is from a book about fluid mechanics. And there they said: "For each closed area the integral vanishes via the area vector of all area elements.". – hallo007 Apr 28 '21 at 16:56
  • You left out very important stuff that came before that sentence. Or the book did. – David K Apr 28 '21 at 17:04
  • Are there words like incompressible flow involved here? – copper.hat Apr 28 '21 at 17:06
  • Yes, they do this but this little topic (appendix) about normal vectors and area vectors is explained in just one page. On this page they don't talk about incompressible flow and there they don't bring this together. – hallo007 Apr 28 '21 at 17:17
  • I may have misunderstood what you meant by "closed". The interpretation in the answer below seems plausible. – David K Apr 28 '21 at 23:27
  • The notation is still a little foreign to my experience too. I have seen $\oint$ for a contour integral but not for a surface integral. Also, it's unclear why the book would use dot product notation in $\underline{n}\cdot dA$ since $dA$ does not act like a vector, and if $dA$ did act like a vector then the dot product would produce a scalar result and the integral of the scalar over the surface would not be zero. – David K Apr 28 '21 at 23:39
  • No. Here $ \underline{n}\cdot dA $ is just a scaled vector. So you are scaling the vector $ \underline{n} $ by $ dA $. But from my side it is also weird writing a scalar factor behind the vector. – hallo007 Apr 28 '21 at 23:53
  • That's the thing, it should just be a scaled vector. And the way to write an integration element like this as a scaled vector is $\underline{n},dA$, not $\underline{n}\cdot dA$. We normally use the dot in something like $\underline{F}\cdot d\underline{A}$, which means something completely different. – David K Apr 30 '21 at 12:40

2 Answers2

4

  1. I assume in this context "closed" surface means the boundary is empty (and everything is nice enough for Stokes theorem to be applied). Now, one of the corollaries of Stokes' theorem is that for any smooth function $f$ and any "nice" surface $S$, \begin{align} \int_{S}\nabla f\,\times d\mathbf{A}&=-\int_{\partial S}f\,d\mathbf{l}. \end{align} Now, let $f_1(x,y,z)=x$, $f_2(x,y,z)=y$ and $f_3(x,y,z)=z$, so that $\nabla f_i=\mathbf{e}_i$ is the $i^{th}$ standard basis vector. Then, \begin{align} \mathbf{e}_i\times\left(\int_S\,d\mathbf{A}\right)&= \int_S\mathbf{e}_i\times d\mathbf{A}=\int_S\nabla f_i\times d\mathbf{A}= -\int_{\partial S}f_i\,d\mathbf{l}=0, \end{align} wherre the last equal sign is because the boundary $\partial S$ is empty. Now, it is easy to verify that if a vector is such that its cross product with each vector in a basis vanishes, then the vector must be to zero vector. Hence, $\int_Sd\mathbf{A}=0$.

  2. The notation $d\mathbf{A}$ for example $\int_SF\,d\mathbf{A}$ means you're integrating the vector-valued function $F\,\mathbf{n}$ with respect to the area element on the surface $S$ (and if you want to get really technical, this is the induced Riemann-Lebesgue measure from the metric tensor induced on $S$ by pullingback the metric tensor in the ambient $\Bbb{R}^3$). Take a look at this answer of mine where I talk about various ways to interpret double integrals; granted they're mostly in the case where the function being integrated is real-valued, not vector-valued, but hopefully that is still helpful.

  3. As we just showed, it is the zero vector, so I'm not sure what else you're looking for. It should seem like a plausible result though, atleast for highly symmetric surfaces like $S$ being the 6 sides of the cube (because the area vectors of opposite sides point in opposite directions, hence cancel out in pairs). Or for the sphere of any given radius $S_r=\{\xi\in\Bbb{R}^3\,:\,\lVert \xi\rVert=r\}$ (because in this case, at any point, there is a diametrically opposite point which will cause the normal vectors to "cancel out").

Note by the way that in proving $(1)$, if we make the additional assumption that $S$ is itself the boundary of some volume $\Omega$ (i.e $S=\partial \Omega$), then a simpler proof can be given by directly applying the divergence theorem: for any basis vector $\mathbf{e}_i$, we have \begin{align} \mathbf{e}_i\cdot \left(\int_Sd\mathbf{A}\right)&=\int_{\partial \Omega}\mathbf{e}_i\cdot d\mathbf{A}= \int_{\Omega}\text{div}(\mathbf{e}_i)\,dV=0. \end{align} Once again, if the inner product of a given vector with respect to every vector in a basis vanishes, then that vector must be the zero vector. This method of proving assumes more (that $S$ is itself the boundary of some region), but the proof is simpler, because it uses the regular form of the divergence theorem, rather than in (1) where we used a corollary of Stokes' theorem (which many of us may not even remember... I certainly had to look it up to refresh my memory on the signs).

peek-a-boo
  • 65,833
  • Why do you use $ \int_S dA $? My integral is $ \int_S d\underline{A} $ and $ dA $ is a surface piece and $ d\underline{A} $ is an area vector. – hallo007 Apr 28 '21 at 21:06
  • 1
    @hallo97 I've tried to use boldface throughout to mean the vector, which is what you have written as $d\underline{A}$. So, $d\underline{A}\equiv d\mathbf{A}\equiv\mathbf{n},dA \equiv \mathbf{\nu},dA$ are all the same thing just different notation (where $\mathbf{n}$ and $\mathbf{\nu}$ are common notation for the unit normal on the surface) – peek-a-boo Apr 28 '21 at 21:08
  • Ok. That was confusing me. Annother question. Why can I write $ e_i\cdot (\int_S dA)=\int_{\partial \Omega} e_i\cdot dA $ and why did you changed the set from $ S $ to $ \partial \Omega $? – hallo007 Apr 28 '21 at 21:19
  • 1
    @hallo97 you can bring the dot product inside simply because of how vector valued integration is defined (i.e intergral of a vector function is the vector whose components are the respective vector components. So, if I want the $i^{th}$ component of the vector integral, I just have to integrate being the $i^{th}$ component. In formulae: $\int_S (f_1,\dots f_k),dA:=(\int_S f_1,dA,\dots \int_S f_k,dA)$). Also, in that paragraoh, I clearly mention we are assuming $S=\partial \Omega$ for some $\Omega$. – peek-a-boo Apr 28 '21 at 21:20
  • Ah I see. I just overread it. And why we get $ 0 $ instead of $ \underline{0} $? – hallo007 Apr 28 '21 at 21:22
  • 1
    after a while, everyone writes $0$ regardless of whether we mean the zero scalar/vector/matrix tensor/function whatever... with some practice we can read from context which meaning is intended. In my proof of (1) in the beginning, I should have written $\mathbf{0}$ for a vector zero, but at the bottom, the scalar $0$ is correct. – peek-a-boo Apr 28 '21 at 21:22
  • Yes, I know what you mean but here it was important at first. But when I look again now at your calculation $ \begin{align} \mathbf{e}i\cdot \left(\int_Sd\mathbf{A}\right)&=\int{\partial \Omega}\mathbf{e}i\cdot d\mathbf{A}= \int{\Omega}\text{div}(\mathbf{e}_i),dV=0. \end{align} $ I would say it is just $ 0 $ and not a "columnvector"? – hallo007 Apr 28 '21 at 23:25
  • (+1) Well written-clear and concise. – Mark Viola Apr 29 '21 at 00:25
1

If I understand your question now, the "area" $A$ (I would rather call it a "surface") "encloses" a finite region of space. If $A$ is the surface of the rigid body in a fluid whose pressure is the same everywhere (not like a body of water on Earth, which has higher pressure in the deeper parts) then the fluid would exert no force on the body and the body exerts no force on the fluid.

If the pressure in the fluid is $1,$ then the vector area element $d\mathbf A = \mathbf n\,dA$ (with $\mathbf n$ facing outward from the body) is an element of the force the body exerts on the fluid, and the integral $$ \int_A d\mathbf A $$ is the total force of the body on the fluid, which is zero. So that's a physical interpretation of the integral.

David K
  • 108,155