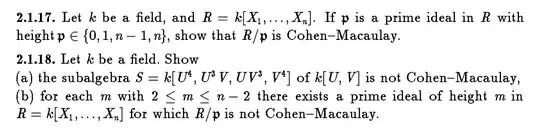Cohen-Macaulayness and regularity of $A/p$

Question

This question claimed (and proved) that if $p$ is a prime ideal of $A=k[x_1,\ldots,x_n]$ with $\operatorname{ht}(p) \in \{0,1,n-1,n\}$, then $A/p$ is Cohen-Macaulay.

Now, let $A$ be a (Noetherian) UFD of Krull dimension $n$ which is Cohen-Macaulay, and let $p$ be a prime ideal of $A$ with $\operatorname{ht}(p) \in \{0,1,n-1,n \}$.

Question 1: Is it true that $A/p$ is Cohen-Macaulay?

My answer: Yes, it is true that $A/p$ is CM, and the same proof holds.

More elaborately:

If $\operatorname{ht}(p)=0$ then $p=(0)$, so trivially $A/p=A/0=A$ is CM.

If $\operatorname{ht}(p)=1$, then $p$ is principal, since a height one prime in a UFD is principal, see wikipedia(11). Then by the nice proposition in this answer, $A/p$ is CM.

If $\operatorname{ht}(p)=n−1$, then $\dim A/p=1$, and one-dimensional integral domains are CM, see wikipedia or MSE.

If $\operatorname{ht}(p)=n$, then $\dim A/p=0$, hence $A/p$ is a field, and fields are CM.

---

Let us concentrate on $A=k[x_1,\ldots,x_n]$ and $p$ a prime ideal of $A=k[x_1,\ldots,x_n]$ with $\operatorname{ht}(p)=1$.

Now again $p$ is principal, but $A/p$ is not necessarily regular. Indeed, $(x^2-y^3)$ is a height one prime of $k[x,y]$ and $k[x,y]/(x^2-y^3)=k[z^2,z^3]$ is CM but not regular (since regular implies normal, but $k[z^2,z^3]$ is not normal, namely, not integrally closed in its field of fractions $k(z)$).

Question 2: What happens if $\operatorname{ht}(p)=n-1$? In that case we have a one-dimensional integral domain $A/p$; is it necessarily regular?.

Question 3: More generally: Could one guarantee regularity of a quotient of $A=k[x_1,\ldots,x_n]$ by a prime ideal $p$ of height different then $\{0,n\}$? Maybe adding assumptions would help?

Thank you very much!

Answer 1

I will answer this question for completeness even though it was several years ago in order to add some references that I could not find myself when I thought about this some weeks ago.

The question that you link in the beginning is the solution to Exercise 2.1.17 in Bruns and Herzog's Cohen–Macaulay rings (screenshot at the end of the answer), which you correctly generalize in Question 1. One of the cases is also discussed in this question. Question 2 you already give a counterexample, as it is noted by Francesco in the comments. The same thing happens with question 3: note that quotienting by a prime ideal in general just means that your variety is irreducible, which is far from implying that it is regular! However, it is an interesting question what happens with Cohen–Macaulayness in quotients by primes of height between 2 and n-2 (which I assume is what you meant).

Exercise 2.1.18 (also in the screenshot) aims to work on this question: it can be proven for each $2\leq m\leq n-2$, there exists a prime $\mathfrak{p}$ of height $m$ whose quotient $k[x_1,\dots,x_n]/\mathfrak{p}$ is not CM. The book leads you to realise the general solution: for each such $m$, there exists a "pinched Veronese subring" $S$ such that $S\cong k[x_1,\dots,x_n]/\mathfrak{p}$, and you can prove that these are not Cohen–Macaulay.

I don't know a general definition of pinched Veronese subring, but in this case I refer to some generalization of the subring $k[U^4,U^3V,UV^3,V^4]\subset k[U^4,U^3V,U^2V^2,UV^3,V^4]$ of Veronese subrings towards which the book hints, where one/the middle generating term is missing. This particular case above is answered here, and is also discussed in Eisenbud's book.