In problems involving coordinate geometry, a lot of the time the solution provided only considers the simplest case and treats it as though the results obtained from it would work for every case. For example, one question asks,
Find the curve for which the area of the triangle formed by the x-axis, the tangent line and radius vector of the point of tangency is equal to $a^2$.
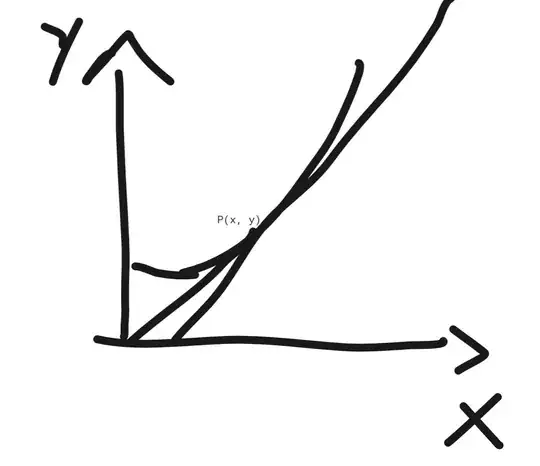
Now the solution in the book uses the simplest case(apologies for the abysmal sketches);
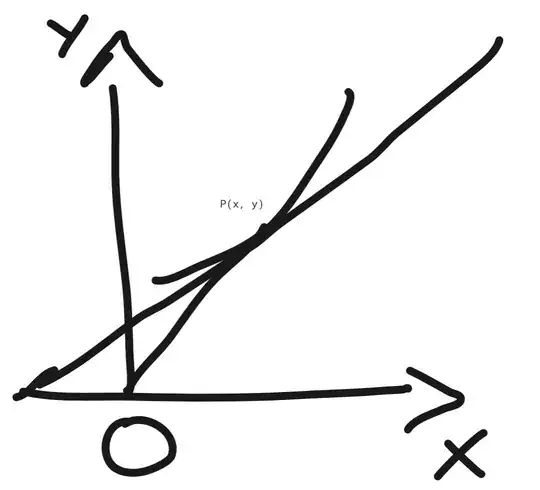
Here and in the following pics, P is the point of tangency. This first case is simple enough, but these are possible, too;
And many more.
Now to find the areas of these triangles, the base has to be found using the subtangent and the abscicca, and each case has it differently; their magnitudes are added or subtracted according to the case.
I could write all of them down and solve the equations, but there probably is a more intuitive way by which the general case can be solved. I say this because I've seen multiple questions like this, and all of them are solved in the book's solutions using just the one case. Which means it's kind of a waste of time to evaluate separate cases, because they're all apparently equivalent.
So is there any such intuition? How can I use it?
EDIT: When you work out the above three cases for the point being in each quadrant, you get the base to be, respectively, $$x-\frac{y}{m}\\ x-\frac{y}{m}\\ \frac{y}{m}-x$$ for the first and fourth quadrants, and the exact negatives of these for the second and third quadrants(where x and y represent the coordinates of the point, and m the slope.). This is what I meant- they are all of almost the same form, and if you take the absolute value, all twelve values are the same. Is there any way to think about these kinds of situations without having to work out each case?