I had recently asked a question about a conjecture in a triangle, and it led me to another question.
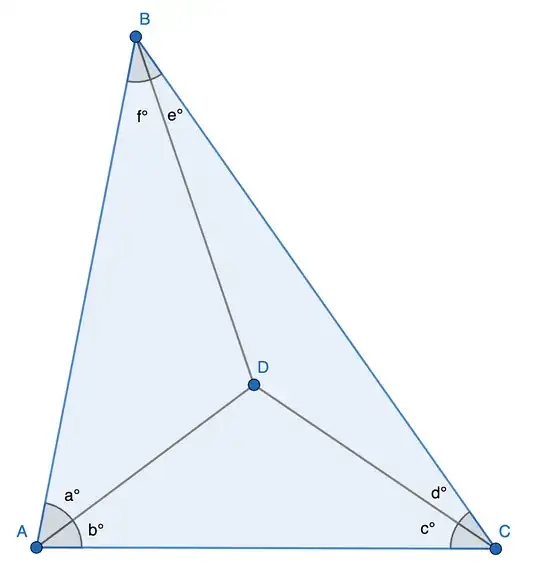
In the non-equilateral triangle below, $CD, AD$, and $BD$ concur at point $D$. The angles $(a, b, c, d, e,$ and $f)$ in degrees are also placed as given in the figure below.
Define a solvable triangle such that: For a triangle like the one in the figure above, given two pairs of adjacent angles (say $a,b$ and $c,d$), if the remaining two angles (say $e,f$) can be found by a synthetic solution using elementary geometry, it is a solvable triangle. (Just to be clear, I have added an example at the end.)
My questions are:
Are all triangles containing integer angled sextuplets solvable triangles?
What is the criterion for being a solvable triangle?
Such a sextuplet must satisfy the Trigonometric Ceva's Theorem:
$$\frac{\sin(a\cdot\frac{\pi}{180})}{\sin(b\cdot\frac{\pi}{180})}\cdot\frac{\sin(c\cdot\frac{\pi}{180})}{\sin(d\cdot\frac{\pi}{180})}\cdot\frac{\sin(e\cdot\frac{\pi}{180})}{\sin(f\cdot\frac{\pi}{180})}= 1$$
We also know that,
$$a+b+c+d+e+f=180°$$
In the comments of their accepted answer to my previous question, @user provided a sextuplet $\frac\pi{180}\{1,30,87,2,29,31\}$ with different integers to work on -I am also sure that there more such sextuplets which consist of different integers.
Here is an example problem using this sextuplet (there are more such triangles that can be formed with this sextuplet):
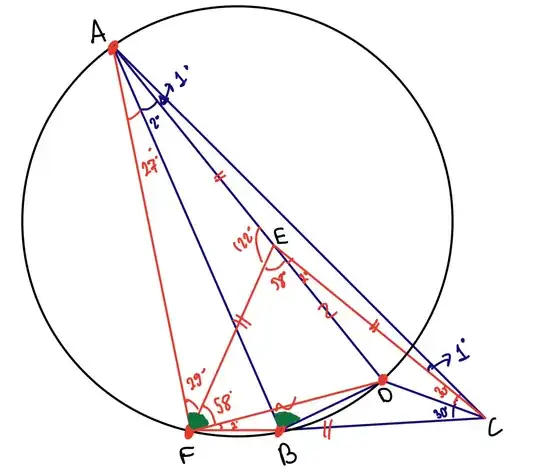
Let $\measuredangle ACD=31°$, $\measuredangle BCD=30°$, $\measuredangle CAD=1°$, $\measuredangle BAD=2°$ in $\bigtriangleup ABC$. Find $\color{green}{\text {$\measuredangle ABD$}}$.
Example Synthetic Solution:
Since the angles are extremely small, I have reproduced the diagram by rescaling the angles (blue line segments represent the original problem and red line segments represent my constructions).
Let’s select a point $E$ on $AD$ such that $AE=CE$ and connect $E$ and $C$, so $\measuredangle ECA=1°$.
Let’s extend $BC$ and select a point $F$ on $BC$ such that $CE=CF$, constructing the equilateral triangle $\bigtriangleup CEF$.
Angle chasing leads us to: $$\measuredangle DEC=2° \; \text{and} \; \measuredangle DEF=58°$$
Let’s connect points $F$ and $D$. Since $CD$ is the angle bisector of the equilateral triangle $\bigtriangleup CEF$, using congruency: $$\measuredangle DFB=2° \; \text{and} \; \measuredangle DFE=58°$$
Since $\bigtriangleup AEF$ is isosceles, $\measuredangle AFE=29°$.
Since $\measuredangle DFB=\measuredangle BAD=2°$, $AFBD$ is a cyclic quadrilateral, which allows us to conclude that:
$$\color{green}{\text {$\measuredangle AFD=\measuredangle ABD=87°$}}$$
I think the $30°$ angle is the critical angle that allowed this solution.
$\\$
The synthetic solution seems to be difficult when $a, b, c, d, e,$ and $f$ are all different integers.
I am not very sure what the appropriate tags are for this question.
Thanks in advance.