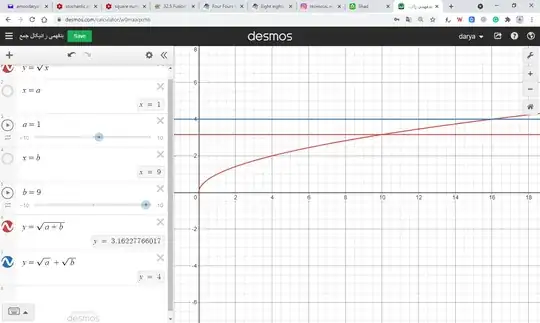
What's wrong about $\sqrt{10} = \sqrt{9 + 1} = \sqrt{9} + \sqrt{1} = 3 + 1 = 4$?
I know that it's logically wrong because $4 \times 4 = 16$, but the syntax to me seems to be healthy as long as I can see, well, of course, because I'm novice and I can't see much, but I think this silly question could have a very detailed and deep answer about what's wrong and what's right in math and how to reason while solving.
Thank you.