$\angle DAB = 10^\circ$, $\angle CAD = 20^\circ$, $\angle CDB = 140^\circ$, $CD = BD$. Find $\angle ABD$

Question

$\angle DAB = 10^\circ$

$\angle CAD = 20^\circ$

$\angle CDB = 140^\circ$

The triangle $\triangle BCD$ is isosceles. $CD = BD$

Find the angle $x$

The answer is $30º$.

Playing with GeoGebra, I found that $AC = AD$. But I don't know how to prove it.

Answer 1

Construct an equilateral triangle $\triangle DCE$ inside of $\triangle ADC$ as follows: 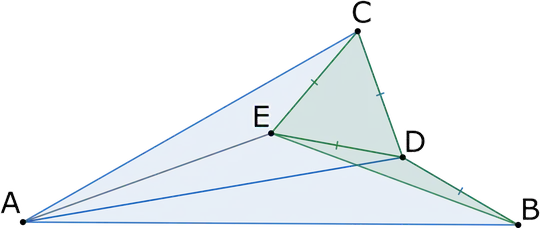We can see that $\angle ADB = 180^\circ - \angle DAB - \angle ABD = 170^\circ - x$ because $\angle DAB = 10^\circ$. Now, because $\angle CDB = 140^\circ$, we now know that $\angle ADC = 360^\circ - \angle ADB - \angle CDB = 50^\circ + x$. So $\angle EDA = \angle ADC - \angle EDC = x - 10^\circ$. (Note that because $\triangle DCE$ is equilateral, we must have $\angle EDC = \angle ECD = 60^\circ$ in particular.) Moreover, $\angle ACE = \angle ACD - \angle ECD = 180^\circ - \angle CAD - \angle ADC - \angle ECD = 50^\circ - x$.

Furthermore, $\angle EDB = \angle EDA + \angle ADB = 160^\circ$. As $|ED| = |DC| = |BD|$, $\triangle EDB$ is isosceles and therefore $\angle EBD = \angle EDB = 10^\circ$. But then $\angle DAB = 10^\circ = \angle DEB$. So $ABDE$ is a cyclic quadrilateral. From that we get that $\angle EAD = \angle EBD = 10^\circ$ and $\angle CAE = \angle CAD - \angle EAD = 10^\circ$ since $\angle CAD = 20^\circ$.

Note that $|AE| = |AE|$, $|ED| = |EC|$ and $\angle EAD = \angle EAC$ in $\triangle AED$ and $\triangle AEC$ respectively. To prove that $\triangle AEC \cong \triangle AED$, we therefore have to prove that it is impossible for one of the angles $\angle AED$ and $\angle AEC$ to be obtuse, and the other acute. This can be seen from the fact that $\angle AED + \angle AEC = 360^\circ - \angle CED = 300^\circ$: if one angle were indeed to be in the interval $(0^\circ, 90^\circ)$ and the other in the interval $(90^\circ, 180^\circ)$, then the sum would not be greater than $270^\circ$, resulting in a contradiction.

From $\triangle AEC \cong \triangle AED$ we at last see that $\angle ACE = \angle ADE$ and as such $50^\circ - x = x - 10^\circ$ or $x = 30^\circ$.

Answer 2

Set $\angle ACD= y, x+y=110^\circ$

For $\triangle ADC$ and $\triangle ADB$:

\begin{align}\frac{DB}{AD}=\frac{\sin 10^\circ}{\sin x}=\frac{CD}{AD}=\frac{\sin 20^\circ}{\sin (110^\circ -x)}\end{align}

\begin{align}\frac{\sin 10^\circ}{\sin 20^\circ}=\frac{sin x}{\cos(x-20^\circ)}\end{align} \begin{align}\tan x=\frac{\cos 20^\circ}{2\cos 10^\circ -\sin 20^\circ}=\frac{\sqrt 3}{3}^*, x=30^\circ\end{align}

EDIT:

\begin{align}\frac{\cos 20^\circ}{2\cos 10^\circ -\sin 20^\circ}=\frac{\cos 20^\circ}{\cos 10^\circ+\cos 10^\circ-\sin 20^\circ}=\frac{\cos 20^\circ}{\cos 10^\circ+\sin 80^\circ-\sin 20^\circ}=\frac{\cos 20^\circ}{\cos 10^\circ+\cos 50^\circ}=\frac{\cos 20^\circ}{2\cos 20^\circ\cos 30^\circ}=\frac{\sqrt 3}{3}\end{align}