Find the X and Y of two points of a rectangle

Question

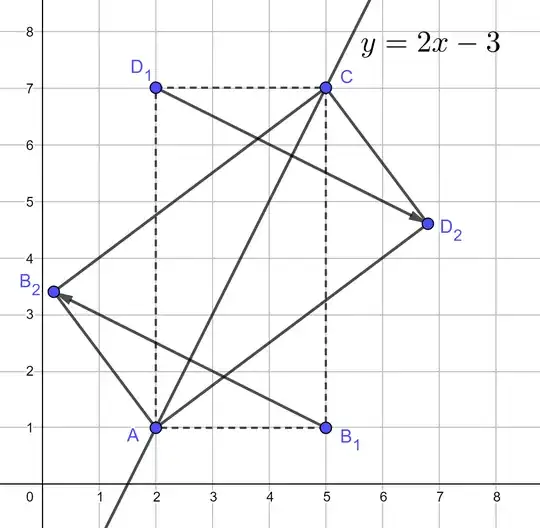
Let $ABCD$ be a rectangle.

Given:

$A(2;1)$

$C(5;7)$

$\overline{BC}=2\overline{AB}$.

I tried to solve it, but after using the Pythagoras theorem I got that $\overline{AB}=\overline{DC}=3$ and $\overline{AD}=\overline{BC}=6$ but I don't know what I do from here.

How can I get points $B$ and $D$? (There are two answers)

score 1 · Answer 1 · answered Apr 02 '21 at 17:14

1

Let $P_x$ denote $x$ coordinate of $P$

Notice $C_x - A_x = 3 = |AB|$,

So, The sides of rectangle are parallel to the grid lines (try to prove this),

Hence $B$ and $D$ are $(5,1) ; (2,7)$

answered Apr 02 '21 at 17:14

Aditya_math

1,887

That's one of the answers, but there is also another answer of D(6.8; 4.6) and B(0.2; 3.4) – The Neighbors Kid Apr 02 '21 at 17:16

score 1 · Accepted Answer · answered Apr 02 '21 at 17:54

For second possibility, the rectangle will be reflection of first one (with sides parallel to gridlines) in the diagonal $AC$ as in the diagram :

Hence the points $B_2,D_2$ will be reflection of $B_1,D_1$ in the diagonal line.

Line $AC$ is $2x-y-3=0$. The reflections of $B_1=(5,1)$ and $D_1=(2,7)$ can be found using the formula mentioned in this MSE post :

$$\frac{x-x_1}{2}=\frac{y-y_1}{-1}=\frac{-2(2x_1-y_1-3)}{2^2+(-1)^2}$$

Find the X and Y of two points of a rectangle

2 Answers2