1

We can regard $\pi_1(X,x_0)$ as the set of basepoint-preserving homotopy classes of maps $(S^1,s_0)\rightarrow(X,x_0$). Let $[S^1,X]$ be the set of homotopy classes of maps $S^1\rightarrow X$, with no conditions on basepoints. Thus there is a natural map $\Phi:\pi_1 (X,x_0)\rightarrow[S^1,X]$ obtained by ignoring basepoints. Show that $\Phi$ is onto if $X$ is path-connected, and that $\Phi([f])=\Phi([g])$ iff $[f]$ and $[g]$ are conjugate in $\pi_1(X,x_0)$. Hence $\Phi$ induces a one-to-one correspondence between $[S^1,X]$ and the set of conjugacy classes in $\pi_1(X)$, when $X$ is path-connected.

We think of $\pi(X, X_0)$ as homotopy classes of basepoint preserving maps $(S^1, s_0) \rightarrow (X, x_0)$. Recall that a map is basepoint preserving iff $f(s_0) = x_0$.

Define $[S^1, X]$ to be homotopy classes of maps $S^1 \rightarrow X$ with no condition on basepoints. The exercise asks us to show that the map $\Phi: \pi_1(X, x_0) \rightarrow [S^1, X]$ is an onto map if $X$ is path-connected.

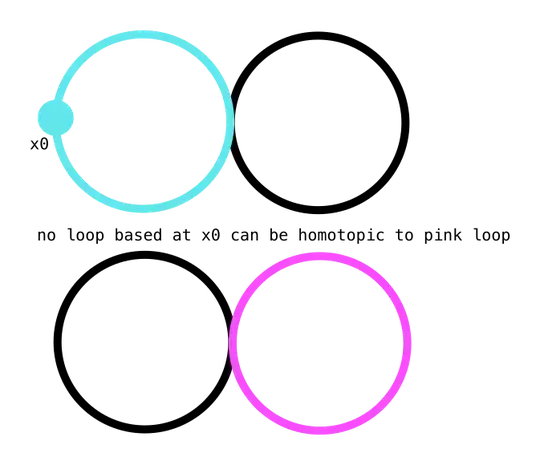
I don't think is true. Consider a wedge of circles. This is path-connected. Now consider all loops based at $x_0$, a point on the left circle that is not on the right circle. In the figure, this is in blue. These loops are in $\pi(X, x_0)$. Now, on the other hand, consider a loop on the circle on the right hand side. In the figure, this loop is in pink. It seems impossible that any blue loop can be homotped into a pink loop.

Indeed, by reading ahead, we know that the fundamental group of the wedge of circles is $W \equiv \mathbb Z * \mathbb Z \simeq \langle a, b\rangle$. All loops on the left circle will be of the form $a^n$, while a loop on the right circle will be of the form $b^m$. The map $\Phi$ that produces all the $a^n$ cannot produce a $b^m$, and thus the map $\Phi$ cannot be surjective.

What am I missing?

enter image description here

Juan Castaño
  • 694
Siddharth Bhat
  • 8,832
  • 1
    The correspondence is between $\pi_1(X,x_0)$ and conjugacy classes, not homotopy classes. – Douglas Molin Apr 02 '21 at 08:24
  • That's the second part of the question, right? I don't even understand how $\Phi$ is onto. – Siddharth Bhat Apr 02 '21 at 08:29
  • 1
    It's the whole question. What you want to check is that the basefree loops you get are conjugate, not that they are homotopic. – Douglas Molin Apr 02 '21 at 08:32
  • So the question is asking me to prove that any loop in $[S^1, X]$ is conjugate to some loop in the image of $\Phi$? I don't understand how the English in the question implies this at all; Clearly my reading comprehension is off. Why does the question say "show that $\Phi$ is onto if $X$ is path-connected, and ... "? – Siddharth Bhat Apr 02 '21 at 08:34
  • 1
    I'm very sorry, I misread it. I will have a think before I say anything more. – Douglas Molin Apr 02 '21 at 08:37
  • 1
    Choose a point in $x_1$ in the pink loop $b$. Let $h$ be the path joining $x_0$ and $x_1$. Then then the path $\beta_h(b)$ is (basepoint-free) homotopic to $b$ (its not hard to draw the homotopy square for this homotopy). – feynhat Apr 02 '21 at 08:52
  • 1
    By $\beta_h$, I mean the change-of-basepoint map. So $\beta_h(b)$ will be $h \cdot b \cdot \overline{h}$. – feynhat Apr 02 '21 at 08:53
  • @feynhat I am quite confused as it is; Could you add the homotopy using the change-of-basepoint map as an answer? I'd be happy to accept it! – Siddharth Bhat Apr 02 '21 at 08:57

2 Answers2

2

Loops based at $x_0$ can be (freely) homotopic to the pink loop. As an example consider the loop starting at $x_0$ which travels along the upper half of the left circle until it reaches the intersection of both circles, then travels once along the pink circle and travels back along the upper half of the left circle to $x_0$.

Paul Frost
  • 87,968
  • What does "freely homotopic" mean? So, as I understand it, this answer asserts that (1) one can deform the pink loop into a loop that "visits" $x_0$ and then makes the pink loop? (2) It is thus homotopic to the pink loop, while being an element of $\pi_1(X, x_0)$? (3) The reason we were able to do this is because we don't need to keep the loop "pinned down" at $x_0$ since we forget basepoints? – Siddharth Bhat Apr 02 '21 at 09:23
  • 1
    @SiddharthBhat Yes. That's what I meant by basepoint-free homotopy. The members of $[S^1, X]$ are basepoint-free homotopy classes of loops. To show that $\Phi$ is surjective you need to show that any such class has a based-loop representative (ie. a member in $\pi_1(X, x_0)$). – feynhat Apr 02 '21 at 09:27
  • @SiddharthBhat Correct. In $\pi_1(X,x_0)$ we only consider homotopies keeping the basepoint fixed, in $[S^1,X ]$ homotopies can move the basepoint arbitrarily. See also https://math.stackexchange.com/q/4044399 . – Paul Frost Apr 02 '21 at 09:34
1

One can write an explicit expression for the homotopy but I am quite convinced by this picture, this picture

where $x_1$ is a point on the pink loop $b$ (more generally suppose $[b]$ is any member of $[S^1, X]$) and $h$ is a path joining $x_0$ and $x_1$. The top edge of the square is $\beta_h(b) = h \cdot b \cdot \overline{h}$.

The only thing that might need some explanation is the green portion.

On the left green portion, we can define the homotopy to be $h$ along the line segment emanating from $x_0$ and meeting the left slant edge. And do something similar on the right green portion.

feynhat
  • 2,010