Questions about SVD, Singular Value Decomposition

Question

I am not a mathematician, so I need to understand what SVD does and WHY more than how it works exactly from the math perspective. (I understand at least what is the decomposition though).

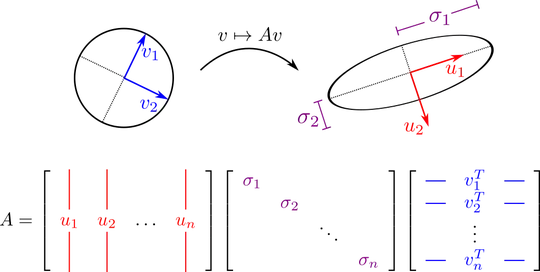
This guy on youtube gave the only human explanation of SVD saying, that the U matrix maps "user to concept correlation" Sigma matrix defines the strength of each concept, and V maps "movie to concept correlation" given that initial matrix M has users in the rows, and movie (ratings) in the columns.

He also mentioned two concept specifically "sci fi" and "romance" movies. See the picture below.

My questions are:

1. How SVD knows the number of concepts. He as human mentioned two - sci fi, and romance, but in reality in resulting matrices are 3 concepts. (for example matrix U - that one with blue titles - has 3 columns not 2).

2. How SVD knows what is the concept after all. I mean, what If i shuffle the columns randomly how SVD then knows what is sci fi, what is romance. I mean, I suppose there is no rule, group the concepts together in the column order. What if scifi movie is the first and last one? and not first 3 columns in the initial matrix M?

3. What is the practical usage of either U, Sigma or V matrices? (Except that you can multiply them to get the initial matrix M)

4. Is there also any other possible human explanation of SVD than the guy up provided, or it is the only one possible function? Matrices of correlations.

Answer 1

Here is a way to understand from a different point of view what the SVD means, using an algorithm based on a balanced weighting between rows and columns.

I will use two slides of the Linear Algebra lectures I have been giving for many years (adapted from its french version):

First slide.

It deals with the following SVD:

$$\underbrace{\begin{pmatrix} 0&1\\1&2\\3&3\end{pmatrix}}_A = \underbrace{\begin{pmatrix} \color{red}{0.1595} & \ \ 0.7077 & \ \ 0.6882\\ \color{red}{0.4520} & \ \ 0.5675 & -0.6882\\ \color{red}{0.8776} & -0.4208 & \ \ 0.2294\end{pmatrix}}_U \underbrace{\begin{pmatrix} \ \ \color{red}{4.8146} & 0\\ 0 & 0.9054\\ 0 & 0\end{pmatrix}}_{\Sigma} \underbrace{\begin{pmatrix}\color{red}{0.6407} & -0.7678\\ \color{red}{0.7678} & \ \ 0.6407\end{pmatrix}^T}_{V^T}$$

This algorithm (not the most efficient) produces, when stopped after a certain number of steps, a numerical approximation of the first singular element $(U_1,V_1,\sigma_1)$ where $U_1$ and $V_1$ are the first columns of $U$ and $V$ resp. and $\sigma_1$ the dominant singular value.

Why does this "alternate balancing" works ? Here is an explanation.

Second slide.

In fact, it is not surprizing that matrices $AA^T$ and $A^TA$ have "poped up". We find back a property that has been used for a long time to introduce the SVD:

If $A$ is $m \times n$ with $m>n$, the $m \times m$ matrix $AA^T$ and the $n \times n$ matrix $A^TA$, being squared symmetric semi-definite positive matrices have the resp. eigendecompositions :

$$AA^T=U \Sigma' U^T \ \ \ \& \ \ \ A^TA=V \Sigma'' V^T\tag{1}$$

with $U$ and $V$ orthogonal matrices and the same eigenvalues (set apart the zero eigenvalues). More exactly, $\Sigma''$ is the upper diagonal block of $\Sigma'$, the remaining (diagonal) entries of $\Sigma'$ being filled by zeroes.

Remarks:

1. Of course, (1) is an immediate consequence of the multiplication of

$$A=U \Sigma V^T \ \ \ \text{by} \ \ \ A^T=(U \Sigma V^T)^T=V \Sigma^T V^T$$

due to the fact that $U^TU=I$ and $V^TV=I$ (orthogonality property).

2. Once $(U_2,V_2,\sigma_2)$ has been obtained, a so-called "deflation" $A'=A-\sigma_1U_1V_1^T$ is operated on matrix $A$, then the same algorithm is applied to $A'$ in order to get the second singular element $(U_2,V_2,\sigma_2)$. Here, from a numerical point of view, there is a drawback for big matrices : deflation accumulates errors. But efficiency and precision are not here our main concerns, our objective being a better insight about what SVD really is...

3. Matrix $\Sigma$ is a kind of "tradeoff" between $\Sigma'$ and $\Sigma''$.

Answer 2

A matrix, $A \in \mathbb{R}^{M \times N}$, maps vectors in $\mathbb{R}^N$ to vectors in $\mathbb{R}^M$ via matrix multiplication, $$v \mapsto A v$$ If you multiply the matrix with every vector on the unit sphere in $\mathbb{R}^N$, the resulting vectors you get out will form an ellipsoid in $\mathbb{R}^M$. The primary axes of the ellipsoid in $\mathbb{R}^M$ are orthogonal. Also, it is possible to prove that the input vectors that get mapped to those primary axes are orthogonal in $\mathbb{R}^N$.

The singular value decomposition $A = U \Sigma V^T$, is an encoding of the sphere and the ellipsoid.

• The left singular vectors, $u_i$, are primary axes of the ellipsoid, except scaled to be unit length.
• The singular values, $\sigma_i$, are the lengths of the primary axes of the ellipsoid
• The right singular vectors, $v_i$, are the unit vectors on the sphere that get mapped to the primary axes of the ellipsoid.

This was all assuming the dimensions of the input and output are the same. But the idea extends to the case where dimensions of the input and output are different ($M \neq N$).

• If the input dimension is larger than the output dimension ($N > M$), then there are $N-M$ orthogonal vectors on the unit sphere that get squashed to zero, but in the other $M$ complementary directions everything is the same as described above.

• If the output dimension is larger than the input dimension ($M > N$), then the output is still an ellipsoid, but it is contained in a $N$-dimensional hyperplane, and is totally flat in the $M-N$ directions complementary to the hyperplane.

Answer 3

I've made the following code to illustrate what I mean about the line of best fit. I hope you find it useful

import numpy as np
import scipy.linalg as la
import matplotlib.pyplot as plt
Adjustable parameters
N = 20           # Number of data points
var1 = 3         # Horizontal stretch factor
var2 = 5         # Vertical stretch factor 
mean1 = 0        # Horizontal mean (distribution)
mean2 = 1        # Vertical mean
line_scale = 5   # determines length of best fit line
#Generate data
R = np.random.rand(2,N)              #Random matrix to generate data
R = np.random.normal(size = (2,N))
A = (R-.5) * np.asarray([[var1],[var2]]) + np.asarray([[mean1],[mean2]])
Plot data
plt.scatter(A[0,:],A[1,:])                 # Plot data points
mu = np.average(A,axis=1)

plt.scatter(mu[0],mu[1],marker='*',s=250)  # Plot data mean (as orange star)
Find best-fit line using SVD
U = la.svd(A)[0]
v = np.reshape(U[:,0],(-1,1))
B = np.hstack((-v,v))*line_scale
plt.plot(B[0,:],B[1,:])
Uncomment to set x and y scales equal
plt.xlim((-5,5))
plt.ylim((-5,5))

Here's an example output. The trendline inferred by the SVD slopes upward, whereas the true trendline should be more horizontal. This can be seen as the effect of the mean (the orange star).

---

Update: this version includes the true best fit line (which requires zeroing the column-mean)

import numpy as np
import scipy.linalg as la
import matplotlib.pyplot as plt
Adjustable parameters
N = 20           # Number of data points
var1 = 3         # Horizontal stretch factor
var2 = 5         # Vertical stretch factor 
mean1 = 0        # Horizontal mean (distribution)
mean2 = 1        # Vertical mean
line_scale = 3   # determines length of best fit line
#Generate data
R = np.random.rand(2,N)              #Random matrix to generate data
R = np.random.normal(size = (2,N))
A = (R-.5) * np.asarray([[var1],[var2]]) + np.asarray([[mean1],[mean2]])
Plot data
plt.scatter(A[0,:],A[1,:])                 # Plot data points
mu = np.average(A,axis=1)

plt.scatter(mu[0],mu[1],marker='*',s=250)  # Plot data mean (as orange star)
mu = np.reshape(mu,(-1,1))
Find best-fit 1-D subspace using SVD
U = la.svd(A)[0]
v = np.reshape(U[:,0],(-1,1))
B = np.hstack((-v,v))*line_scale
plt.plot(B[0,:],B[1,:])
Find best-fit line (1-D affine subspace) using PCA
M = A - mu
U = la.svd(M)[0]
w = np.reshape(U[:,0],(-1,1))
C = mu + np.hstack((-w,w))*line_scale
plt.plot(C[0,:],C[1,:])
Uncomment to set x and y scales equal
plt.xlim((-5,5))
plt.ylim((-5,5))

Sample output: