15

Is it possible to divide the equilateral triangle into 4 pieces and assemble a square with these four pieces, provided that one or two pieces are flipped over to the other side? In other words, I want a mirror reflection of one or two pieces. If this riddle has no solution, I would like to find proof.

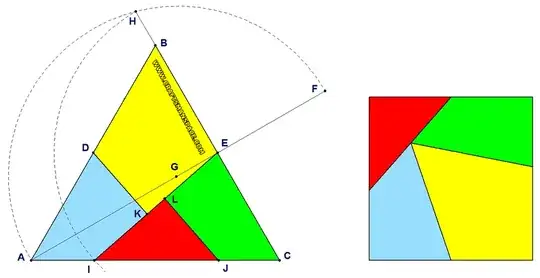
Let me remind original solution: enter image description here

Mind that the blue and green elements in the picture above do not have the same shape. So it is not possible to flip them both to the other side:

Dudeney’s solutions to haberdasher's problem exact measures of sections

Original riddle of Henry Dudeney:

https://www.gutenberg.org/files/27635/27635-h/27635-h.htm#p26

Here is a solution for 5 elements, which of course does not satisfy me.

https://puzzling.stackexchange.com/q/79981/53127

Reason why I seek this solution

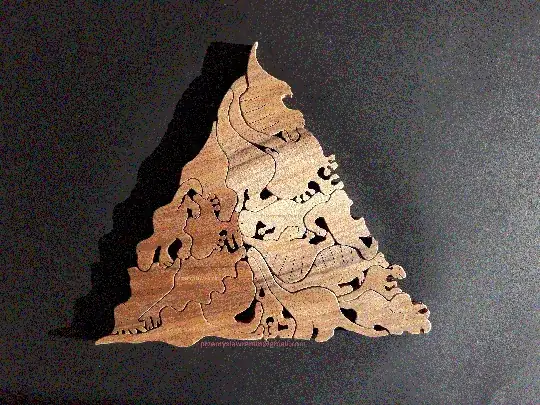
The two pictures below may give you a context as to why I posted this question. I am a carpenter, I design and create dinosaur wooden puzzles. This one is based on Henry Dudney's dissection pattern. Assembling the triangle is already deity level difficulty. Unless familiar with Dudney's dissection, the wood grains lead you astray to square. However, the necessity of flipping any piece to the other side is what makes puzzles difficult even for a deity. Here is a video showing an example of dinosaur flip. Even my friends who know that I use a flip to obscure the puzzle, they cannot see that two shapes are complementary, if one is flipped. That is my life goal. Design a puzzle that nobody can solve :-)

Przemyslaw Remin Dinosaur Puzzle Square

enter image description here

Przemyslaw Remin
  • 51
  • 2
    My day job currently involves a project about common polygonal dissections, so I'll definitely be sharing your di(no)ssections w/colleagues. :) ... As for the task at hand: So far, I've only come up with a 4-piece solution that requires flipping all 4 pieces. ;) I'll have to give this more thought. (FYI: The Equidecomposability Theorem guarantees that that you could cut an arbitrary piece from the square, and its mirror image from the triangle, and then find a non-flippy common dissection of the remaining shapes. However, it doesn't guarantee a dissection with just a few "nice" pieces.) – Blue Oct 04 '23 at 00:03
  • @Blue The proof that there is no such solution is also at stake. Anyway, meanwhile as we do not know if the solution exists, it would be nice to learn how to construct dissection with an arbitrary piece and its mirror image with 5 pieces. – Przemyslaw Remin Oct 06 '23 at 12:52
  • 2
    I have to give more thought to either direction. :) ... I mentioned the Equidecomposability Thm only for the sake of completeness. It says that any two polygons of equal area —say, the square and triangle w/some shape and its mirror-shape removed— have a common dissection, but it makes no promises about the number —or nice-ness— of pieces involved. The result lends itself to brute-force algorithmic dissections, but those typically involve lots & lots & lots of slivers and tiny triangles; see, eg, Smirnov & Epstein's "Scissors Congruence" applet. – Blue Oct 06 '23 at 15:36
  • 1
    @Blue Love the di(no)ssections wordplay. – Tito Piezas III Oct 26 '23 at 17:16

0 Answers0