Let $(f_n)_{n\in\mathbb{N}}$ be a sequence of functions with $f_n:\mathbb{R}\rightarrow[0,1]$ for all $n\in\mathbb{N}$ and $f:\mathbb{R}\rightarrow[0,1]$ continuous such that $\lim_{n\rightarrow\infty}f_n(x)=f(x)$ for all $x\in\mathbb{R}$. Is it now possible to show that $f_n$ converges uniformly to $f$?
Asked
Active
Viewed 5,695 times
6
-
Hint: When looking for counter examples, it is sometimes easiest to start off with a picture. Can you draw a sequence of non-negative, piecewise smooth functions $f_n$ with the following properties: $f_n(0)=f_n(1)=0$ for all $n$, $f_n$ attains a maximum value of 1 at $1/(n+1)$, and $f_n(x)$ is zero outside of $[0,1]$. Given a simple such example, it might not be hard to write down a formula. I'll draw such a sequence for you in a few hours, if no one else has answered this. – Mark McClure May 29 '13 at 12:00
-
Ok, I get it. For example \begin{equation} f_n(x):=\left{\begin{array}{cl} \exp(1)\exp(-\frac{1}{1-((n+1)x-1)^2}), & \mbox{for }x\in\left[0,\frac{2}{n+1}\right]\ 0, & \mbox{otherwise} \end{array}\right.\end{equation} – stroem May 29 '13 at 14:16
-
That is very clever! It's even smooth, I believe. I'll show you my example in a min. – Mark McClure May 29 '13 at 14:22
2 Answers
19
Your example, $$ f_n(x) = \begin{cases} e^{1-1/({1-((n+1) x-1)^2})} & 0<x<\frac{2}{n+1} \\ 0 & \text{otherwise,} \end{cases} $$ behaves something like so:
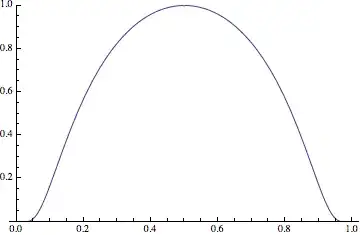
I think it's crystal clear that this is a continuous (even differentiable, I think) sequence of functions that converges pointwise to zero. The convergence clearly can't be uniform, since there's always a point where the value of $f_n$ is $1$.
The example I had in mind looks something like this:
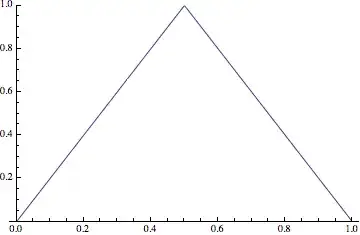
Note that the graph consists of just straight line segments, so it's quite simple to write down a piecewise formula for this. In fact:
$$ f_n(x) = \begin{cases} (n+1) x & 0<x<\frac{1}{n+1} \\ 2-(n+1) x & \frac{1}{n+1}<x<\frac{2}{n+1} \\ 0 & \text{otherwise}. \end{cases} $$
I emphasize, though, that (in my approach, at least) the picture comes first.
Mark McClure
- 31,496
6
That's not necessary true, standard example is $f_n(x) = x^n$ for $x\in[0,1)$ and $f_n(x) = 0$ otherwise. They converge point-wise to $f\equiv 0$ but not uniformly. What you have instead is Dini's theorem:
If $(f_n)$ are continuous functions, and they converge to a continuous function $f$ point-wise and monotonically on a compact set, then they converge uniformly to that function.
SBF
- 36,568