I have the transition matrix $$P= \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ \frac14 & \frac14 & \frac12 \end{pmatrix}$$
and I have to determine the period of each state, compute $f_{2,2}{(n)}$ for each $n\geq 1$ and compute $p_2(X_n=3)$ I think $f_{2,2}{(n)} = p_{(2,3)}p_{(3,2)}=1ยท\frac14=\frac14$ but I am not sure and the last part I have $p_i(X_n=j)=p_{i,j}{(n)}$ but I don't know how to do it
thank you
$p_{i,j}^{(n)}$ can be found from the $n^{th}$ power of the transition matrix computed with spectral decomposition of $P=V\Lambda V^{-1}$ s.t., $P^n=V\Lambda^nV^{-1}$,
Here we have
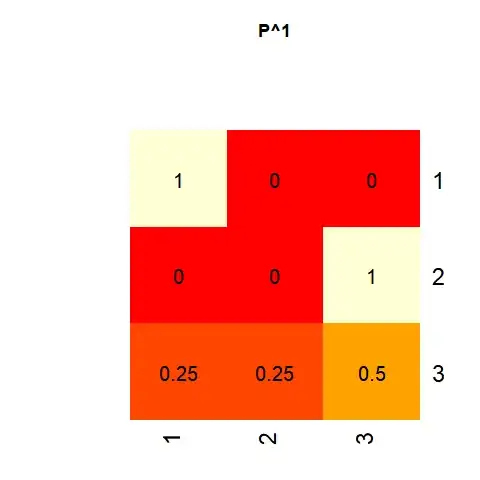
$P = \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ \frac14 & \frac14 & \frac12 \end{pmatrix} $
$V = \begin{pmatrix} 0.5773503 & 0 & 0\\ 0.5773503 & 0.7774375 & 0.9554226\\ 0.5773503 & 0.6289602 & -0.2952418 \end{pmatrix} $
$\Lambda = \begin{pmatrix} 1 & 0 & 0\\ 0 & 0.809017 & 0\\ 0 & 0 & -0.309017 \end{pmatrix} $
Value of $p_{2,2}^{(n)}$ can be obtained from $P^n(2,2)$ s.t., for n = 2,
$ P^2 = \begin{pmatrix} 1.000 & 0.000 & 0.0 \\ 0.250 & 0.250 & 0.5 \\ 0.375 & 0.125 & 0.5 \end{pmatrix} $
s.t., $p_{2,2}^{(2)}=\frac1 4$ and $p_{2,3}^{(2)}=\frac1 2$
Note that 1 being the absorbing state of the Markov chain, eventually $p_{i,1}^{(n)}=1, \forall{i}$ and $p_{i,j}^{(n)}=0, \forall{j \neq 1}$ when $n \to \infty$
The following animation shows how $p_{i,j}^{(n)}$ changes with increasing $n$.
