Drawing a triangle in a unit circle

Question

This is a question that I derived for a long time ago. It asks if we draw a triangle in a unit circle does all arc lengths $(\alpha ,\beta ,\theta)$ and sides of triangle $(a,b,c)$ can be rational numbers? Intuitively I believe that the rationality does not hold but I can't derive a proof. Do you have any ideas?

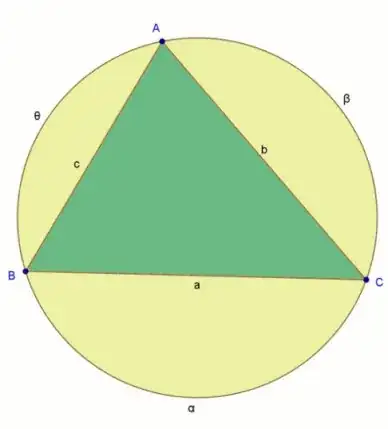
enter image description here

score 6 · Accepted Answer · edited Apr 13 '17 at 12:20

6

$\alpha + \beta + \theta = 2 \pi$, so they can't all be rational.

You might want to write the arc lengths as $\alpha \pi, \beta \pi, \theta \pi$, in which case $\alpha + \beta + \gamma = 2$, and it gets slightly more interesting.

The answer is still no.

(WLOG, we have $0 \leq \alpha, \beta, \gamma \leq 2$.) This arises because $a= 2| \sin \frac{\alpha\pi}{2}|$, which is rational if and only if $\frac{\alpha}{2} \in \{ 0, \frac{1}{6} ,\frac{1}{2}, \frac{5}{6}, 1\} $. This is known as Niven's Theorem.

The only way to get $\frac{\alpha}{2} + \frac {\beta}{2} + \frac{\gamma}{2} = 1$ is then to require that $\alpha\beta\gamma=0$ (slight checking involved), which is the degenerate cases (that I'm ignoring). These cases correspond to either having a point on the circumference, or a chord of the circle.

edited Apr 13 '17 at 12:20

Community

1

answered May 28 '13 at 19:39

Calvin Lin

77,541

Can you elaborate on th esecond "no"? After all there is the degenerate case with $a=b=2$, $c=0$. – Hagen von Eitzen May 28 '13 at 19:43
@newzad I think we can both agree that $\pi$ and $1/\pi$ are irrational, but is $\pi\cdot1/\pi$? ;-) – obataku May 28 '13 at 19:45
Imagine $\alpha=k_12\pi$,$\beta=k_22\pi$,$\theta=k_32\pi$ and $k_1+k_2+k_3=1$ but $\alpha,\beta,\theta$ are rational. – newzad May 28 '13 at 19:46
@HagenvonEitzen I've added it in, and stated why we get the degenerate cases (of which there are a few more consisting of chords). – Calvin Lin May 28 '13 at 19:58
@oldrinb: $\pi$ and $1/\pi$... where's the love for $\sqrt{2}$? – Eric Tressler May 28 '13 at 20:01
@newzad With this change, I've answered your question in my second part. – Calvin Lin May 28 '13 at 20:01

Drawing a triangle in a unit circle

1 Answers1