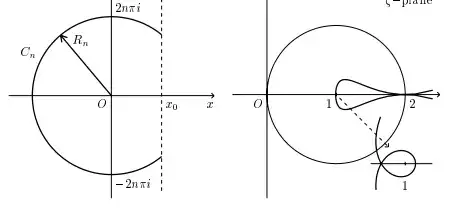
What is the image of the circle $z=2n\pi e^{i\theta}$ under the map $w=1+e^z$

Question

Can somebody help me with this problem?

In the book, it says that

${(i)}$ the region $0 \le x\le x_0$ and $z$ on the circle $C_n$, the image points $w=1+e^z$ all lie to the right and slightly below the point $w=2$, for $y$ sufficiently close to $2n\pi$, that is, for $n$ sufficiently large. Hence $$|1+e^z|\ge2$$

${(ii)}$Then for $Re(z)=x \lt 0$ the values of the function $w=1+e^z$ are inside the circle $|w-1|=1$. This is because for $Re(z)=x \lt 0$ we have $|w-1|=|e^xe^{iy}|=|e^x|\ \lt 1$. As the value of $y$ goes from $2n\pi$ down to $(2n-1)\pi$, the image spiral half a revolution with modulus $$|1+e^z|\ge 1+ e^{2n\pi \cos(\phi)}\cos(2n\pi \sin\phi)\gt b \gt 0$$ for $x=2n\pi \cos\phi$ and $y=2n\pi \sin\phi$

As $y$ goes from $(2n-1)\pi$ down to $(2n-2)\pi$, the images $w$ spiral away from the origin half a revolution. For $y \lt 0$ it is the same story but spiraling outward.

I don't understand the first part ${(i)}$ and in the second part I can only understand why for $Re(z)=x \lt 0$ the values of the function $w=1+e^z$ are inside the circle $|w-1|=1$. The rest is really confusing. I would really appreciate some help

I think I understand that for $Re(z)=x \lt 0$ the values of the function $w=1+e^z$ are inside the circle $|w-1|=1$. This is because for $Re(z)=x \lt 0$ we have $|w-1|=|e^xe^{iy}|=|e^x|\ \lt 1$ — J.Dane, Mar 03 '21 at 16:21
For $n=\tfrac1{2\pi}(1+\operatorname{W}(\tfrac1{\mathrm{e}}))\approx0.20347395$ the circle and its image are externally tangent. — g.kov, Mar 04 '21 at 03:42
Because for this value of $n\quad$ $2n\pi\exp(\mathrm{i}\cdot0)=1+\exp(2n\pi\exp(\mathrm{i}\cdot\pi))$ holds. — g.kov, Mar 05 '21 at 14:15

What is the image of the circle $z=2n\pi e^{i\theta}$ under the map $w=1+e^z$

0 Answers0