Approach to address errors from float precision limits by its storage limit

Question

Background

In computer, the limited float precision due to the storage limit e.g. 64 bit can cause problems. Trying to understand what approaches are available and being used to cope with or overcome the precision limitations.

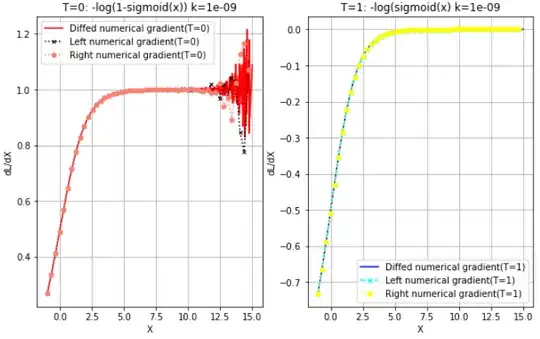
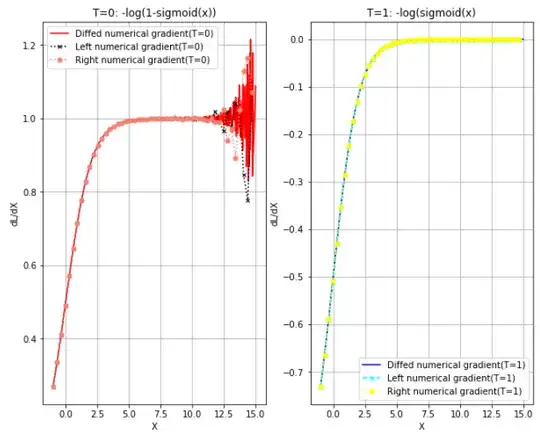
The original issue is numpy - why numerical gradient log(1-sigmoid(x)) diverges but $\log(\operatorname{sigmoid}(x))$ does not?. While trying to implement a numeric gradient (f(x+k)-f(x-k)) / 2k of the logistic log loss function, encountered a problem of float calculation gets unstable. When $f(x)$ and $k$ gets smaller such as 1e-8, $\log(\operatorname{sigmoid}(x))$ started diverging while $\log(\operatorname{sigmoid}(x))$ does not.

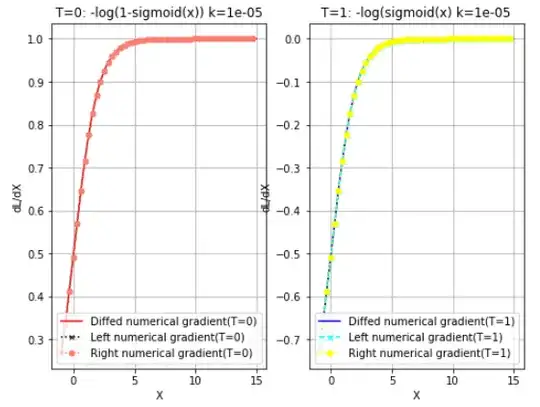
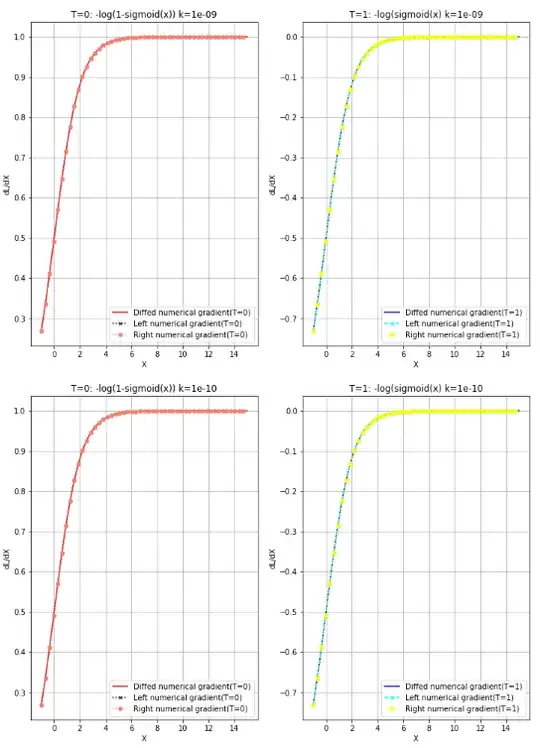
When the values are relatively large such as 1e-5, the issue does not happen, at least in the range of x.

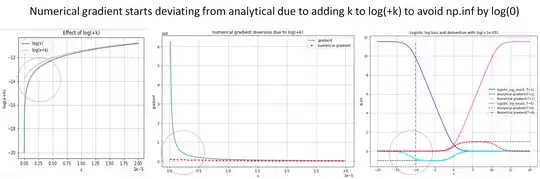
The reason trying to make k smaller is to prevent log(0) to become np.inf by adding a small number u e.g. 1e-5 but log(x+1e-5) causes a deviation of numerical gradient from the analytical one. To minimize the impact, I try to make it smallest possible and start having this issue.

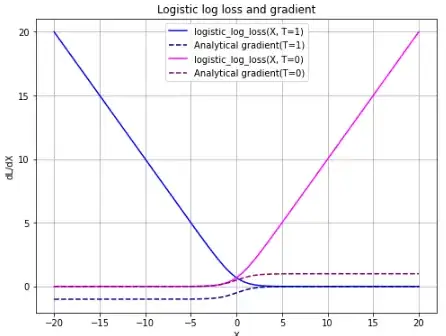
Logistic log loss functions

y in the figure is binary true/false label T and p is the activation sigmoid(x),

Question

I believe there are science and engineering fields which require high precision calculations. I like to understand

What kind of float numerical calculation problems exist.
Which mathematics topics or areas to look into.
What approaches are being used to address limited precision/storage issues in computing.

Code

Logistic log loss and analytical gradient.

import numpy as np
import inspect
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def __sigmoid(X):
    return 1 / (1 + np.exp(-1 * X))
def __logistic_log_loss(X: np.ndarray, T: np.ndarray):
    return -(T * np.log(__sigmoid(X)) + (1-T) * np.log(1-__sigmoid(X)))
def __logistic_log_loss_gradient(X, T):
    Z = __sigmoid(X)
    return Z-T
N = 1000
left=-20
right=20
X = np.linspace(left,right,N)
T0 = np.zeros(N)
T1 = np.ones(N)
--------------------------------------------------------------------------------
T = 1
--------------------------------------------------------------------------------
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(
    X,
    __logistic_log_loss(X, T1),
    color='blue', linestyle='solid',
    label="logistic_log_loss(X, T=1)"
)
ax.plot(
    X, 
    __logistic_log_loss_gradient(X, T1),
    color='navy', linestyle='dashed',
    label="Analytical gradient(T=1)"
)
--------------------------------------------------------------------------------
T = 0
--------------------------------------------------------------------------------
ax.plot(
    X, 
    __logistic_log_loss(X, T0), 
    color='magenta', linestyle='solid',
    label="logistic_log_loss(X, T=0)"
)
ax.plot(
    X, 
    __logistic_log_loss_gradient(X, T0),
    color='purple', linestyle='dashed', 
    label="Analytical gradient(T=0)"
)
ax.set_xlabel("X")
ax.set_ylabel("dL/dX")
ax.set_title("Logistic log loss and gradient")
ax.legend()
ax.grid(True)

Numerical gradient

def t_0_loss(X):
    return [
        #logistic_log_loss(P=sigmoid(x), T=0)
        -np.log(1.0 - __sigmoid(x)) for x in X 
    ]
def t_1_loss(X):
    return [
        #logistic_log_loss(P=sigmoid(x), T=1)
        -np.log(__sigmoid(x)) for x in X 
    ]
N = 1000
left=-1
right=15
Numerical gradient
(f(x+k)-f(x-k)) / 2k
k = 1e-9
X = np.linspace(left,right,N)
fig, axes = plt.subplots(1, 2, figsize=(10,8))
--------------------------------------------------------------------------------
T = 0
--------------------------------------------------------------------------------
axes[0].plot(
    X,
    ((np.array(t_0_loss(X + k)) - np.array(t_0_loss(X - k))) / (2*k)),
    color='red', linestyle='solid',
    label="Diffed numerical gradient(T=0)"
)
axes[0].plot(
    X[0:-1:20],
    ((np.array(t_0_loss(X + k)) - np.array(t_0_loss(X))) / k)[0:-1:20],
    color='black', linestyle='dotted', marker='x', markersize=4,
    label="Left numerical gradient(T=0)"
)
axes[0].plot(
    X[0:-1:20],
    ((np.array(t_0_loss(X)) - np.array(t_0_loss(X - k))) / k)[0:-1:20],
    color='salmon', linestyle='dotted', marker='o', markersize=5,
    label="Right numerical gradient(T=0)"
)
axes[0].set_xlabel("X")
axes[0].set_ylabel("dL/dX")
axes[0].set_title("T=0: -log(1-sigmoid(x))")
axes[0].legend()
axes[0].grid(True)
--------------------------------------------------------------------------------
T = 1
--------------------------------------------------------------------------------
axes[1].plot(
    X,
    ((np.array(t_1_loss(X + k)) - np.array(t_1_loss(X - k))) / (2*k)),
    color='blue', linestyle='solid',
    label="Diffed numerical gradient(T=1)"
)
axes[1].plot(
    X[0:-1:20],
    ((np.array(t_1_loss(X + k)) - np.array(t_1_loss(X))) / k)[0:-1:20],
    color='cyan', linestyle='dashed', marker='x', markersize=5,
    label="Left numerical gradient(T=1)"
)
axes[1].plot(
    X[0:-1:20],
    ((np.array(t_1_loss(X)) - np.array(t_1_loss(X - k))) / k)[0:-1:20],
    color='yellow', linestyle='dotted', marker='o', markersize=5,
    label="Right numerical gradient(T=1)"
)
axes[1].set_xlabel("X")
axes[1].set_ylabel("dL/dX")
axes[1].set_title("T=1: -log(sigmoid(x)")
axes[1].legend()
axes[1].grid(True)

Numerical analysis texts usually contain a discussion of this. I suspect older ones may be better than newer ones, as floats used to be $32$ bits and have only $7$ digits of precision or so. Subtractive cancellation was much more of a problem then. If you lose $4$ digits of $7$ it is a much bigger deal than if you lose $4$ digits of $16$. One very useful technique is to find the singular part and subtract it analytically. Then the cancellation goes away. — Ross Millikan, Feb 28 '21 at 04:34
@RossMillikan, thanks for the pointer. Will look into subtractive cancellation. If you know good classic textbooks, kindly suggest, as a good classic book is a rare-find. — mon, Feb 28 '21 at 06:12
If you think about what you were taught about subtracting numbers with a given number of significant figures, subtracting two that are close loses precision. So if you do $123.456-123.123=0.333$ your input has six significant figures but the output has only three. The fractional error increases by a factor $1000$ or so. When you start with $16$ digits like today's longs that isn't so bad, but when you start with only $7$ it is a problem. Numerical Recipes has some discussion. — Ross Millikan, Feb 28 '21 at 15:16
There are some questions here on catastrophic cancellation, eg https://math.stackexchange.com/q/1920525/207316 Also see https://en.wikipedia.org/wiki/Loss_of_significance It's always good to rearrange calculations to avoid or minimise these effects, when that's possible, but there's also the option of using numbers with higher precision. Python has various ways to do that, from the standard decimal module, to 3rd party libraries like mpmath. And then there's SageMath... — PM 2Ring, Mar 05 '21 at 11:07

mon · Answer 1 · 2021-03-05T10:52:18.407

Solution by Reza.B.

Let z=1/(1+p), p= e^(-x). You can see then log(1-z)=log(p)-log(1+p), which is more stable in terms of rounding errors (we got rid of division, which is the main issue in numerical instabilities).

Reformulation

$ \begin{align*} P&=exp(-X) \\ log(exp(-X)) &= -X \\ Z &=sigmoid(X) = \frac {1}{1+exp(-X)} = \frac {1}{1+P} \\ log(Z) &= log(\frac {1}{1 + exp(-X)}) \\ &= log(1) - log(1+exp(-X)) \\ &= -log(1+P) \\ \\ log(1-Z) &= log(\frac {exp(-X)}{1+exp(-X)})\\ &= log(P)-log(1+P) \end{align*} $

Then the logistic log loss function is reformulated as:

$ \begin{align*} L &= - \left[ \; Tlog(Z) + (1-T)log(1-Z) \; \right] \\ &= Tlog(1+P) - log(P) + log(1+P) +Tlog(P) - Tlog(1+P) \\ & = (T-1)log(P) + log(1+P) \\ &= (1-T)X + log(1+P)\\ &= (1-T)X + log(1+exp(-X)) \\ \\ L(T=0) &= X + log(1+exp(-X))\\ L(T=1) &= log(1+exp(-X))\\ \end{align*} $

Result

The errors have been resolved.

def t_0_loss(X):
    L = X + np.log(1 + np.exp(-X))
    return L.tolist()
def t_1_loss(X):
    L = np.log(1 + np.exp(-X))
    return L.tolist()
%%timeit
((np.array(t_0_loss(X + k)) - np.array(t_0_loss(X - k))) / (2k))
((np.array(t_1_loss(X + k)) - np.array(t_1_loss(X - k))) / (2k))

599 µs ± 65.6 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Previous erroneous version was:

47 ms ± 617 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Approach to address errors from float precision limits by its storage limit

Background

Logistic log loss functions

Question

Code

Logistic log loss and analytical gradient.

--------------------------------------------------------------------------------

T = 1

--------------------------------------------------------------------------------

--------------------------------------------------------------------------------

T = 0

--------------------------------------------------------------------------------

Numerical gradient

Numerical gradient

(f(x+k)-f(x-k)) / 2k

--------------------------------------------------------------------------------

T = 0

--------------------------------------------------------------------------------

--------------------------------------------------------------------------------

T = 1

--------------------------------------------------------------------------------

1 Answers1

Reformulation

Result