2

I am wondering if there is a mathematical term for this, since I'm trying to search up algorithms that deal with these sort of points/regions, but I am having difficulty finding what I'm looking for.

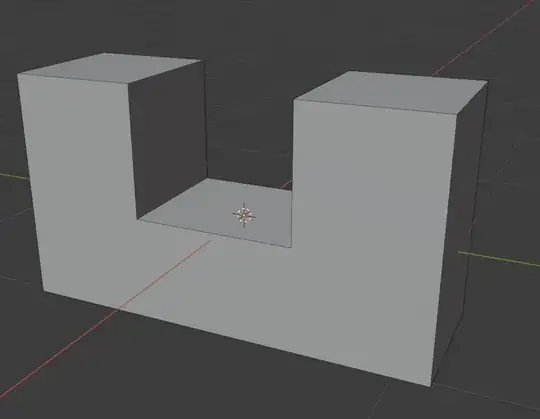
Suppose you have a 3D surface. Indents like the ones highlighted in orange here consist of points that (aside from the boundary) will never appear on the edge of the surface's silhouette, and thus have no impact on said edge of the silhouette, when viewed from any position and any angle. My question is, does a name for such points/regions other than just "indents" exist?

Image of a cube with dents in each face.

Similarly, these semi-spherical indents can be removed without impacting the silhouette (apologies for the image quality; I know these sort of look like they could be semi-spherical bumps depending on lighting/shadow direction, but I assure you they're indents going into the volume). Picture of a 3D cloud-like object with semispherical indents.

However, other "concavities", like the ones shown here, do affect the silhouette, and should not be included in any such definition.

Picture of a shape that is kind of like a 3D letter U.

This question is similar to Name for a body that can be completely described using its silhouettes, which seems to be asking about the name of a body that does not contain any such regions. This is something I'd also be interested in, if anyone has such an answer (the original question has some answers in the comments, but they do not work very well for web searches). However, I'm more interested in names for the indents themselves, if such names exist.

FilmCoder
  • 31
  • 1
    I don't think there is a name, but those indents have no effect on the convex hull. So that is one way to describe them. – Joseph O'Rourke Feb 28 '21 at 01:10
  • @JosephO'Rourke I suppose so, but the "indent" in the second image also has no effect on the convex hull, but does have an effect on the silhouette, so I'd still have to distinguish further. – FilmCoder Feb 28 '21 at 01:33
  • My phrasing was unclear. In the 2nd example, there is a projection direction such that the shape and the hull of the shape differ. Whereas this is not the case in the 1st example: any projection of the shape and the same projection of the hull are identical. – Joseph O'Rourke Feb 28 '21 at 01:59
  • 1
    Not sure whether it will help but there's a fair amount known about the extent to which knowledge of the projections of a convex set determines the set. I used to think about things like this but it would take me a while to find the relevant literature now. – Ethan Bolker Feb 28 '21 at 02:30
  • @JosephO'Rourke Ah, I see. But in the case of the 2nd, you could add a dent-like indent similar to what's in the 1st, and then its projections and convex hull are both the same even though the indentless-version meets the desired criteria while the indented one does not? Unless I misinterpret. In any event, though, thanks for the suggestion! – FilmCoder Oct 07 '24 at 01:06

2 Answers2

1

I asked the same question, and posted the below self-answer, on the Computer Graphics StackExchange, but I guess I forgot to do the same here. Below is the answer (slightly edited) from the CG StackExchange, in case anyone with the same question comes across this post but not the other one in their web search:

After a fair bit of reading and skimming through papers, I have yet to find a good definition other than "indent" for what I want to remove, but I have found answers to pretty much everything else.

The concept of a "Visual Hull" is what I was looking for regarding a mesh that doesn't have these indents. While the Wikipedia page, and a bunch of other resources, usually just refer to visual hulls created from a finite set of viewpoints, e.g. a set of real-life cameras, Laurentini, who introduced the term "Visual Hull", also introduces a term "External Visual Hull" to refer to one created using every possible viewpoint outside of the convex hull [1]. This will have the exact same silhouette as the original mesh when viewed from any position outside the convex hull at any angle, so it was exactly what I was looking for.

[1] also contains an algorithm for computing the external visual hull for polyhedra, but it is sorta brute-force and is $O(n^{12})$. In [2], Petitjean introduces a much more efficient algorithm for polyhedra, and Bottino and Laurentini also describe a more efficient algorithm in [3]. In addition to these algorithms for polyhedra, other works by Laurentini also discuss algorithms for doing the same for curved objects, surfaces of revolution, etc. I have yet to come across anyone actually implementing these algorithms, though (other than the 2D version).

If someone reading this wants to look these up for themselves, then in addition to the below citations, I would like to note that even if you don't normally have access to papers, e.g. through a post-secondary institution, all of these seem to be publicly available. You can download [1] from ResearchGate here, download [2] from ResearchGate here (though I have no clue why different authors are listed for it than Petitjean), and [3] can be found in Google Books.

Citations:

[1] Laurentini, Aldo. (1994). The Visual Hull Concept for Silhouette-Based Image Understanding. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 16. 150-162. 10.1109/34.273735.

[2] Petitjean, S. (1998). A computational geometric approach to visual hulls. International Journal of Computational Geometry & Applications, 8(04), 407-436.

[3] Bottino, Andrea & Laurentini, Aldo. (2006). Retrieval of Shape from Silhouette. 10.1016/S1076-5670(05)39001-X.

FilmCoder
  • 31
0

Each indentation is a pyramidal frustum (a pyramid with a smaller, similar pyramid lopped off the top), as shown below:

enter image description here

Nate
  • 189
  • Sorry, I should have been more careful in wording what I meant by "name for this sort of concave region." I meant a term for any sort of deformation that doesn't affect the "external visual hull" (as defined/linked in my self-answer), because I was having trouble web-searching for an algorithm that removed such indents without knowing what to call them. I've edited my question with an example of a non-pyramidal concavity, but now that I've found an algorithm, knowing their name is something I can live without. Nonetheless, thanks for the answer, and sorry again for my poor wording. – FilmCoder Oct 08 '24 at 19:09