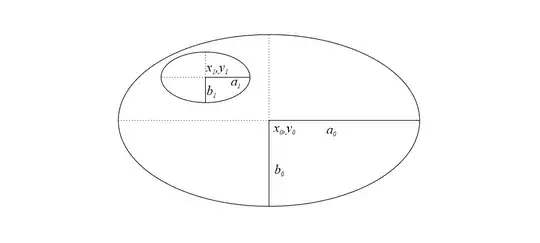
I have two ellipses which are both not rotated, but have different sizes. I want to know if the smaller ellipse 1 is fully inside the larger ellipse 0. In my special case both ellipses have the same axis ratio, so $a_0/b_0=a_1/b_1$, but I doubt this makes a difference for the calculation.
I have started to work on a solution, but I am not so sure if this is the right approach and if it will ultimately lead to success. Here is what I have come up with so far:
The radius of ellipse 0 can be calculated for any point on the ellipse as
$$ r_0=\sqrt{(x-x_0)^2+(y-y_0)^2} $$ The general equation for an ellipse gives a relation between $x$ and $y$ for points on the ellipse.
$$ \frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1 $$
$$ (y-y_0)^2=b*\sqrt{1-\frac{(x-x_0)^2}{a^2}} $$
This can be used to calculate radius of both ellipses depending on the x coordinate.
$$ r_0 = \sqrt{(x-x_0) + b_0^2(1-\frac{(x-x_0)^2}{a_0^2})} $$
$$ r_1 = \sqrt{(x-x_1) + b_1^2(1-\frac{(x-x_1)^2}{a_1^2})} $$
To calculate the distance $s$ between both ellipses at a certain $x$ coordinate, we simply have to add the distance $d_{01}$ between the center points to radius 1 and subtract this from radius 0.
$$ s=r0 - (d_{01} + r1) $$ where $$ d_{01} = \sqrt{(x_1-x_0)^2 + (y1-x_0)^2} $$
Now I have an equation where $s$ only depends on $x$. My idea is to get the minimum of $s$ through the first derivative. If the minimum is non-negative, ellipse 1 is inside or on ellipse 0. If it is negative, part of ellipse 1 is outside ellipse 0.
Here are my questions:
- Am I on the right way so far?
- Is calculating the minimum for s the right approach?
- Do I have a chance to actually calculate the minimum of $s$?
Note: Ther is a similar question here, but I think my case is much simpler because the ellipses are not rotated similar.