1

I have recently read the following problem:

Bob and Jane agree to meet at a known location between 1pm and 2pm. The problem is that neither of them know what time the other will arrive.

We may assume that both of them are equally likely to arrive at any time between 1pm and 2pm.

Assume Bob is prepared to wait 15 minutes for Jane to arrive before leaving. And Jane is prepared to wait 15 minutes for Bob to arrive before she leaves.

What is the probability that they meet?

I tried my hand at the problem but I don't know what did I do wrong:

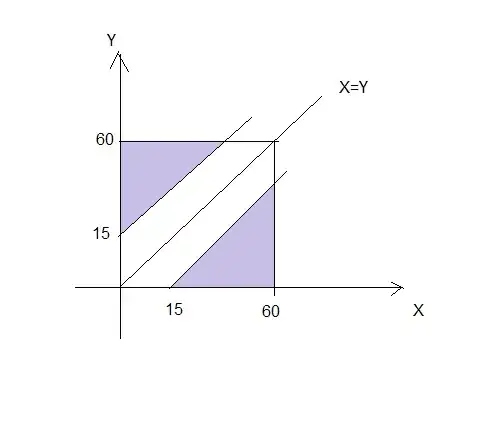
Let $X$ and $Y$ be the arriving time of Bob and Jane $t$ minutes after 1pm respectively, then $X,Y\sim U[0,60]$. Let $A$ be the event that they meet, then by the law of total probability, we have

$$P(A)=\int_0^{60}P(A|X=x)f(x)\,dx$$

Now $f(x)=F'(x)=(x/60)'=1/60$, hence

$$P(A)=\frac{1}{60}\int_0^{60}P(A|X=x)\,dx$$.

$$P(A)=\frac{1}{60}\left( \int_0^{45}P(Y\in [x,x+15])\,dx + \int_{45}^{60}P(Y\in [x,60])\,dx\right)$$

$$P(A)=\frac{1}{60}\left( \int_0^{45}\frac{x+15-x}{60-0}\,dx + \int_{45}^{60}\frac{60-x}{60-0}\,dx\right)=\frac{7}{32}.$$

But the answer is $7/16$. I would like to ask what's wrong with my argument, thank you so much in advance. I would also like to ask is there any other ways to solve this? Thank you.

Ishigami
  • 2,202

2 Answers2

1

A simple drawing will get you the right solution, without integrals

enter image description here

The probability they meet is the white area dvided by the total area of $60^2$. To calculate the interested area is easier to calculate the area of the two purple triangle...thus simply

$$1-\left(\frac{45}{60}\right)^2=\frac{7}{16}$$

tommik
  • 33,201
  • 4
  • 17
  • 35
1

Draw a square in the Cartesian coordinate plane with vertices at $(0,0), (1,0), (1,1), (0,1)$. The horizontal value represents the random time when Bob arrives, in hours after 1 PM. The vertical value represents the random time when Jane arrives, also in hours after 1 PM. So the point $(0.5, 0.25)$ represents Bob arriving at 1:30 PM and Jane at 1:15 PM.

Now, what is the set of points in this square such that Bob and Jane meet? Clearly, they meet if and only if $|X - Y| \le 0.25$, where $X$ and $Y$ are the arrival times of Bob and Jane, respectively. What does the region defined by this inequality look like? What is its area? What is its area as a fraction of the total area of the square?

Now, if you perform this geometric exercise, it might give you insight as to where your computation went wrong. If you were to perform it correctly, the integral would look like this, where I am using units of hours rather than minutes:

$$\int_{x=0}^{1/4} \Pr[0 \le Y \le x + 1/4] \, dx + \int_{x=1/4}^{3/4} \Pr[x - 1/4 \le Y \le x + 1/4] \, dx \\+ \int_{x=3/4}^1 \Pr[x - 1/4 \le Y \le 1] \, dx.$$ But of course, it is easier to exploit symmetry and compute the complementary probability via the single integral $$1 - 2 \int_{x=0}^{3/4} \Pr[x + 1/4 < Y \le 1] \, dx.$$

In essence, your calculation only considers the case where Bob arrives before Jane, thus the condition in your integrand $Y \in [x, x + 15]$. Jane could arrive before Bob and still meet, so $Y \in [x - 15, x + 15]$ is appropriate whenever $x \in [15, 45]$. So this is why your probability evaluates to $7/32$: you are missing exactly half of the total probability, the missing component being the outcomes in which Jane arrives before Bob.

heropup
  • 143,828