Stereographic Projection: Cartography Applications

Question

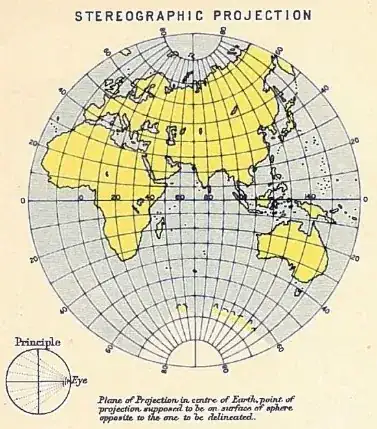
Compared to the Mercator's, which is also conformal, how does the Stereographic projection help in areas such as navigation? Or any application besides simply mapping polar areas, although I would prefer answers on the polar aspect.

Additionally, from Wikipedia:

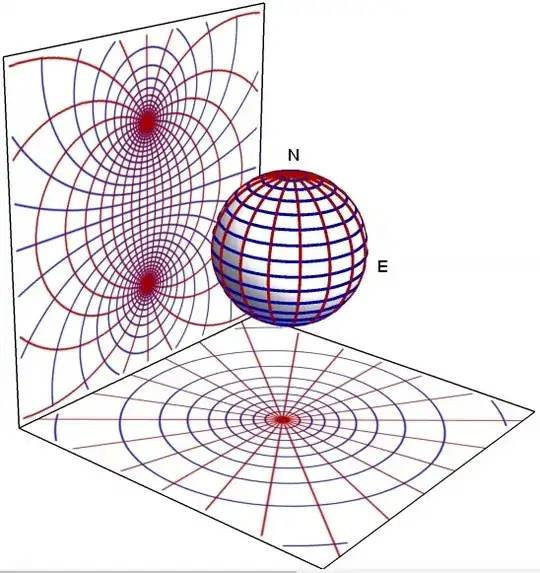
"When the projection is centered at the Earth's north or south pole, it has additional desirable properties: It sends meridians to rays emanating from the origin and parallels to circles centered at the origin".

Why are these desirable qualities? How would it benefit one in any hypothetical situation?

This may not be strictly math related, but any ideas where the stereographic projections' properties could be utilized to solve a problem would still be appreciated.

Edit: Any suitable scenario where its properties can be of use would suffice, it can be very bizarre, but I would prefer it to be related to navigation or locations on Earth.

Answer 1

You consider stereographic projection from North pole.

But I would like to stress the fact that, when the center of projection is done from a point $E$ on the equator, the following pattern is generated:

(Figure taken from this article) explaining the following kind of map where meridians and parallels are "rendered" as two families of orthogonal circles:

with the advantage of minimal deformations along the equator (Figure taken from Oxford Advanced Atlas 1936). This technique had been already used by Mercator in this wonderful map:

(a testimony of the fact that Mercator was mastering other projections than the one he is famous for).

An interesting article about stereographic projection, its history and an application to another scientific field (geology) can be found here

Answer 2

Cartography benefit is significant. Also easy to calculate mappings.

If we consider a small patch like a state on the globe its geographical mapping from sphere surface onto a plane at south pole SPp has an approximately constant magnification. But the angles are preserved (conformal but not isometric). It is useful for GIS and GPS assisted navigation on land.

If the earth's curvature can be neglected.. its small area map is represented on flat SPp tangent plane faithfully.

Corresponding angles do not change in magnitude except for $\phi \to \pi -\phi $ reckoned from meridian. Large loxodromes are mapped to logarithmic spirals along rhumb lines, very useful in ship navigation.

Small circles ( radius small compared to earth's radius ) project to perfect circles on SPp.

When entire Lat/Long lines map is slid by $ 90^{\circ}$ ( so N-S poles axis is along a diameter of equator plane) projection from north pole point light NPl casts a bipolar coordinate map or net.

Properties of circle inversions is useful and interesting.

3d printed surface models cast interesting angle preserving shadow projections on SPp cast from NPl.