This problem had came to a Facebook post. Given that the left angles are given (with only 40° angle on the upper right triangle,find the angle x . What I did us to make equilateral triangles but it seems I still don't get two angles to get the vale of x . Can anyone give me a solution ???
2 Answers
We can easily solve this by making some clever constructions of some points $X$, and $Y$ in the labelled diagram below;
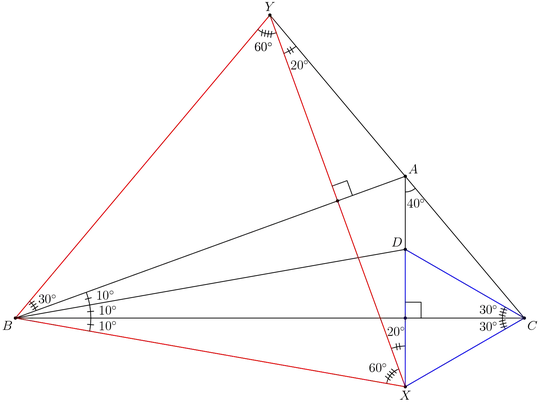
Note that in the diagram, the triangle you gave is $\triangle ABC,$ and $X$ is produced by reflecting $D$ over $BC$, and $Y$ is constructed so that $BX=BY=BD,$ and $\triangle BXY$ is equilateral.
Note that since $\angle ABX=\angle ABY,$ thus $X$ is the reflection of $Y$ over $AB.$ We know that by Angle Chasing that $\angle BAX=90^\circ-\angle ABC=70^\circ,$ thus by properties of reflection, we know that $\angle BAY=70^\circ$ as well.
But then we have;
$$\angle YAC=\angle YAB+\angle BAX+\angle XAC=70^\circ+70^\circ+40^\circ=180^\circ.$$
Hence, $Y$ lies on $AC.$ We know that $\angle YCB=50^\circ=\angle YBC,$ thus $\triangle YBC$ is isosceles, and thus $YC=YB=YX.$
Hence, $\triangle XYC$ is also isosceles. We will now show that the side length of the lateral sides is equal to the side length of the lateral sides of the isosceles triangle $\triangle XBD,$ note that $XY=XB,$ so the claim is proven.
Now we will prove that $\triangle XYC\cong\triangle XBD$ by showing that $\angle XBD=\angle XYC.$ Note that $\angle XBD=20^\circ$ by the construct, and we have; $$\angle XYC=90^\circ-\angle BAY=20^\circ.$$
Thus, the claim is proven and the two triangles are congruent by SAS.
We know by Congruence that $XD=XC.$ But since $CD=CX,$ the $\triangle CDX$ is equilateral, and the result follows by noting that; $$\angle BCD=90^\circ-CDX=30^\circ.$$
- 1,379
-
1Nice solution. Synthetic solutions are always beautiful. As a side note for future, I noticed that without a diagram people seem to be more reluctant to read entries. – krazy-8 Feb 03 '21 at 09:41
-
1Or, after getting $YC=YX=XB$, you can say that points $B,X$ and $C$ lie on the circle with centre $Y$ and radius $YX$. Hence, $\angle DCB=\angle BCX=\frac{1}{2}\angle BYX=30^{\circ}$ – Limestone Feb 03 '21 at 14:06
-
2@DRSKMOBINULHAQUE, Nice observation! That is definitely another way to proceed. – MathMinded Feb 03 '21 at 15:56
-
@AbhinavNegi Thanks. – Limestone Feb 03 '21 at 16:30
-
1@Abhinav Negi where's x and y in your diagram ?? And your diagram doesn't match on the photo ,where are the angles 70 and 40 there ?? – Denver Feb 04 '21 at 22:28
-
@Denver, I am sorry, I added the wrong diagram to this question, now it is fixed. – MathMinded Feb 05 '21 at 08:37
This is a different problem, but it follows the same principles with this problem. In these problems there are two methods to pick from: Synthetic geometry or trigonometry. Although synthetic solutions are more beautiful, they are harder to come up with. To obtain a synthetic solution you need to create isosceles triangles until you end up with an equilateral triangle that can be used to solve the problem or can be used to obtain a congruency.
A more practical theorem is Trigonometric Ceva's Theorem. (The proof of this theorem is done by applying the law of sines to the three triangles , and multiplying all the obtained expressions.) To apply the theorem just multiply the ratios of the sines of the angles at each vertex respectively: $$\frac{\sin(40°)}{\sin(70°)}×\frac{\sin(10°)}{\sin(10°)}×\frac{\sin(x)}{\sin(50° - x)}= 1$$ Rearranging: $$\sin(40)×\sin(x)=\sin(70°)×\sin(50° - x)= 1$$ From here, the answer turns out to be, $$x=30°.$$
- 2,294
