1

Can every Maximal Planar Graph be represented by 'inner' and 'outer' triangulations of a regular polygon? For example for n vertices, draw a regular polygon with n vertices and n edges. Triangulate the inside with n-3 edges and triangulate again on the outside without repeating connections, another n-3 edges. 3n-6 in total. A proof seems to be obtained by taking a 'starting triangle' in the Maximal Planar Graph, adding a new vertex which joins two of the existing vertices, but doesn't enclose a vertex and repeating until all vertices are included, none should be 'inside'. Perhaps this representation would be useful in some situations. Is the 'proof' valid?

RobPratt
  • 50,938
John Hunter
  • 691
  • 4
  • 13

1 Answers1

5

The proof is not valid. In particular, to add a new vertex, it doesn't just need to join two existing vertices, but ones that are adjacent around the polygon built so far; there is no guarantee that such a vertex exists.

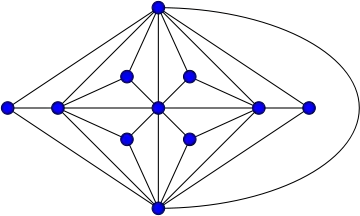
The statement is not always true, either. The smallest counterexample is the Goldner–Harary graph shown below:

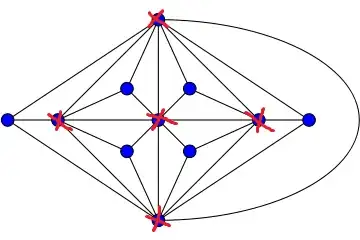
enter image description here

In this maximal planar graph, there simply is no cycle of length $n$ that visits every vertex once. A quick way to see that is to look at what happens when we delete the $5$ vertices marked with an $X$ below:

enter image description here

The result is $6$ isolated vertices. However, if you have an $11$-gon and delete any $5$ of its vertices, you'll leave the remaining $6$ vertices in $5$ or fewer pieces; there will be some edges between them left. So this graph cannot have an $11$-gon inside it. (In other words, the Goldner-Harary graph is not Hamiltonian because it's not $1$-tough.)

Misha Lavrov
  • 159,700