Does the following lower bound improve on $I(q^k) + I(n^2) > 3 - \frac{q-2}{q(q-1)}$, where $q^k n^2$ is an odd perfect number?

Question

Let $N = q^k n^2$ be an odd perfect number with special prime $q$ satisfying $q \equiv k \equiv 1 \pmod 4$ and $\gcd(q,n)=1$.

Define the abundancy index $$I(x)=\frac{\sigma(x)}{x}$$ where $\sigma(x)$ is the classical sum of divisors of $x$.

Since $q$ is prime, we have the bounds $$\frac{q+1}{q} \leq I(q^k) < \frac{q}{q-1},$$ which implies, since $N$ is perfect, that $$\frac{2(q-1)}{q} < I(n^2) = \frac{2}{I(q^k)} \leq \frac{2q}{q+1}.$$

By considering the negative product $$\bigg(I(q^k) - \frac{2(q-1)}{q}\bigg)\bigg(I(n^2) - \frac{2(q-1)}{q}\bigg) < 0,$$ since we obviously have $$\frac{q}{q-1} < \frac{2(q-1)}{q},$$ then after some routine algebraic manipulations, we arrive at the lower bound $$I(q^k) + I(n^2) > 3 - \frac{q-2}{q(q-1)} = \frac{3q^2 - 4q + 2}{q(q - 1)}.$$

Now, a recent MO post improves on the lower bound for $I(n^2)$, as follows: $$I(n^2) > \bigg(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1} + 1}{q^{k+1}}\bigg)$$

Added February 3, 2021 - 8:10 PM (Manila time) Here is a quick way to show the improved lower bound for $I(n^2)$. We have $$I(n^2)=\frac{2}{I(q^k)}=\frac{2q^k (q - 1)}{q^{k+1} - 1}=\frac{2q^{k+1} (q - 1)}{q(q^{k+1} - 1)}=\bigg(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1}}{q^{k+1} - 1}\bigg)$$ $$=\bigg(\frac{2(q-1)}{q}\bigg)\bigg(\frac{(q^{k+1} - 1) + 1}{q^{k+1} - 1}\bigg)=\bigg(\frac{2(q-1)}{q}\bigg)\bigg(1 + \frac{1}{q^{k+1} - 1}\bigg)$$ $$>\bigg(\frac{2(q-1)}{q}\bigg)\bigg(1 + \frac{1}{q^{k+1}}\bigg)$$ since $q^{k+1} > q^{k+1} - 1$. But, of course, we obtain $$I(n^2)>\bigg(\frac{2(q-1)}{q}\bigg)\bigg(1 + \frac{1}{q^{k+1}}\bigg)=\bigg(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1} + 1}{q^{k+1}}\bigg).$$ QED.

Repeating the same procedure as above, we have the negative product $$\Bigg(I(q^k) - \left(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1} + 1}{q^{k+1}}\right)\Bigg)\Bigg(I(n^2) - \left(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1} + 1}{q^{k+1}}\right)\Bigg) < 0.$$

This implies, after some algebraic manipulations, that $$I(q^k) + I(n^2) > \frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}}.$$

But WolframAlpha says that the partial fraction decomposition of the new lower bound is given by $$\frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}} = \frac{3q^2 - 4q + 2}{q(q - 1)} + \frac{2(q - 1)}{q^{k+2}} - \frac{q}{(q - 1)(q^{k+1} + 1)}.$$

So essentially, my question boils down to:

QUESTION: Is it possible to produce an unconditional proof (that is, for all $k \geq 1$ and for all special primes $q \geq 5$) for the following inequality? $$\frac{2(q - 1)}{q^{k+2}} > \frac{q}{(q - 1)(q^{k+1} + 1)}$$

MY ATTEMPT

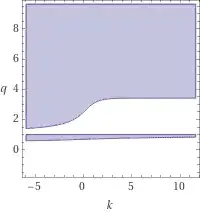
I tried to ask WolframAlpha for a plot of the above inequality, it gave me the following GIF image:

So it does appear that the inequality is unconditionally true, which would mean that the new lower bound for $I(q^k) + I(n^2)$ improves on the old. Is it possible to prove this analytically?

And lastly: Based on this answer to a closely related question, since we appear to have obtained an improved lower bound for $I(q^k) + I(n^2)$, can we then say that there is indeed an integer $a$ such that $k \leq a$?

Answer 1

And lastly: Based on this answer to a closely related question, since we appear to have obtained an improved lower bound for $I(q^k) + I(n^2)$, can we then say that there is indeed an integer $a$ such that $k \leq a$?

I think that we cannot.

In the following, I'll explain the reason why I think that we cannot.

In the answer, I wrote

"If you get an improved lower bound for $f(k)$, then you can say that there is an integer $a$ such that $k\le a$ "

where $f(k)=I(q^k) + I(n^2)$.

Also, in a comment below the answer, I wrote

"if you get an improved lower bound $g(q)$, then from the above fact, we see that there is only one $k=k_0$ such that $f(k)=g(q)$. Then, we have $k\le \lfloor k_0\rfloor$ "

where "the above fact" is the fact that $f(k)$ is decreasing.

In short, we can say that there is an integer $a$ such that $k\le a$ if we get a function $g(q)$ (which is a fuction only on $q$) such that $$I(q^k)+I(n^2)\ge g(q)\gt 3 - \frac{q-2}{q(q - 1)}$$

---

Now, let us see what you've got.

Let $$G(k,q)=\frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}}$$

You have $$I(q^k) + I(n^2) > G(k,q)\gt 3 - \frac{q-2}{q(q - 1)}$$ which is correct since

$$I(q^k) + I(n^2)-G(k,q)=\frac{ (q- 4)q^{k+2}+2 q^{k + 1} + (3 q - 4 )q + 2}{q^{k+2}(q - 1) (q^{k + 1} - 1) (q^{k + 1} + 1)}\gt 0$$

$$G(k,q)-\bigg(3 - \frac{q-2}{q(q - 1)}\bigg)=\frac{ (q - 4) q^{k + 2} +2 q^{k + 1} + 2( q - 2 )q + 2}{q^{k+2}(q - 1) (q^{k + 1} + 1)}\gt 0$$

Also, we have $$\frac{\partial G(k,q)}{\partial k}=-\frac{ (q- 4) q^{2 k + 3}+ 2 q^{2 k + 2}+ 4( q- 2)q^{k + 2} +4 q^{k + 1} + 2( q - 2) q + 2}{q^{k+2}(q - 1) (q^{k + 1} + 1)^2}\ln q\lt 0$$ $$\lim_{k\to\infty}\bigg(I(q^k) + I(n^2) \bigg)=\lim_{k\to\infty}G(k,q)= 3 - \frac{q-2}{q(q - 1)}$$

These imply that you don't get a function $g(q)$ (which is a fuction only on $q$) such that $$I(q^k)+I(n^2)\ge g(q)\gt 3 - \frac{q-2}{q(q - 1)}$$

So, I think that you cannot say that there is an integer $a$ such that $k\le a$.

---

Added :

I'm going to add another explanation with graphs.

Let $$f(k)=I(q^k) + I(n^2),\qquad G(k)=\frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}},$$ $$Q=3 - \dfrac{q-2}{q(q - 1)}$$ where $q,Q$ are seen as constants.

Since we see that $f(k)\gt G(k)\gt Q$ holds for all $k,q$ and that both $y=f(k)$ and $y=G(k)$ are decreasing with $\displaystyle\lim_{k\to\infty}f(k)=\displaystyle\lim_{k\to\infty}G(k)=Q$, we see that their graphs are as follows :

Now, if you take a fixed positive integer $k=k'$, then we have the following :

This explains why you cannot say that $$f(k)\gt G(k′)$$ holds for all $k$.

---

Added 2 :

I'm going to add more explanations with steps :

(1) $f(k)\gt G(k)\gt Q$ holds for all $k,q$.

(2) Both $y=f(k)$ and $y=G(k)$ are strictly decreasing.

(3) $\displaystyle\lim_{k\to\infty}f(k)=\displaystyle\lim_{k\to\infty}G(k)=Q$.

(4) If we let $k=k'$ where $k'$ is a fixed positive number larger than $1$, then $G(k')$ is entirely in terms of $q$ alone.

(5) $Q\lt G(k')\lt f(1)$

(6) It follows from $(2)(3)$ that, for any $Y$ satisfying $Q\lt Y\lt f(1)$, there exists only one $k$ such that $f(k)=Y$.

(7) It follows from $(5)(6)$ that there exists only one $k$ such that $f(k)=G(k')$. Let $k_0$ be this $k$.

(8) For $k\lt k_0$, we have $f(k)\gt G(k')$.

(9) For $k\ge k_0$, we have $f(k)\le G(k')$.

(10) It follows from $(8)(9)$ that $f(k)\gt G(k')$ does not hold for all $k$.

---

Added 3 :

You seem to think that the following claim is true :

Claim : If there are two functions $f(x),g(x)$ such that $$f(x)\gt g(x)\gt 1$$ holds for all $x\gt 0$, then there is a fixed positive integer $m$ such that $f(x)\gt g(m)$ holds for all $x\gt 0$.

This claim is false. Take $f(x)=\dfrac 1x+1$ and $g(x)=\dfrac{1}{x+1}+1$ for which $f(x)\gt g(x)\gt 1$ holds for all $x\gt 0$, but $f(x)\gt g(m)$ does not hold for $x\ge m+1$.

Answer 2

Suppose to the contrary that there exists an integer $k \geq 1$ and a (special) prime $q \geq 5$ such that $$\frac{q}{(q-1)(q^{k+1}+1)} \geq \frac{2(q-1)}{q^{k+2}}.$$ This inequality is equivalent to $$q^{k+3} \geq 2(q-1)^2 (q^{k+1}+1) = 2q^{k+1} - 4q^{k+2} + 2q^{k+3} + 2q^2 - 4q + 2,$$ which in turn is equivalent to $$0 \geq q^{k+3} - 4q^{k+2} + 2q^{k+1} + 2q^2 - 4q + 2 = q^{k+2} (q - 4) + 2q^{k+1} + 2q(q - 2) + 2 > 0,$$ a contradiction.

We therefore conclude that $$\frac{2(q-1)}{q^{k+2}} > \frac{q}{(q-1)(q^{k+1}+1)}$$ for all integers $k \geq 1$ and all (special) primes $q \geq 5$.

Hence, the new lower bound $$I(q^k) + I(n^2) > \frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}}$$ does indeed improve on the old lower bound $$I(q^k) + I(n^2) > 3 - \frac{q-2}{q(q - 1)} = \frac{3q^2 - 4q + 2}{q(q - 1)}.$$

It remains to be seen whether this implies that there does exist an integer $a$ such that $k \leq a$, if $q^k n^2$ is an odd perfect number with special prime $q$.