8

Let $L/\mathbb{Q}$ be a finite Galois extension of degree n, let $\mathcal{O}_{L}$ be the ring of integers of $L$, By Dedekind lemma we have that

$\mathfrak{p}=\mathfrak{b}_{1}^{e}...\mathbb{b}_{g}^{e}$ where $ \mathfrak{b}_{i} \in \mathcal{O}_{L}$ and $\mathfrak{p}$ $\in $$\mathbb{Z}$ Since this extension is Galois we have $gfe=[L:\mathbb{Q}]=n$ where $e$ is the ramification index and $f$ is the inertia degree which is given by $f_{i}=[\mathcal{O}_{L}/\mathfrak{b} :\mathbb{Z}/\mathfrak{p}]$

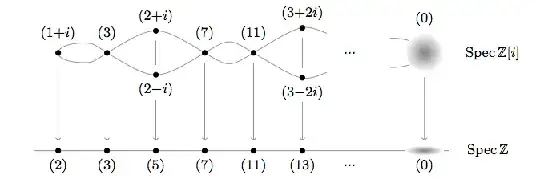
we know that $\mathfrak{p}$ is ramified if $e >1 $, I am asking is there a geometric way to know whether a prime ideal is ramified or not? if it exists can you apply it on this picture (give any example)enter image description here Also, I want to know what is the geometric interpretation of the inertia degree and the ramification index ?

Aster Phoenix
  • 682
  • 1
    I wrote this answer to a similar question : https://math.stackexchange.com/questions/2618017/geometric-interpretation-of-ramification-of-prime-ideals?rq=1 Does this help ? About the question if we can see ramification in the picture : this is not so easy because the picture is already very schematic. I believe the point $(1+i)$ should have been marked differently because this is the only ramified point and is indeed not so different from $(3), (7), (11)...$. I prefer the Mumford's picture (see the linked thread) for that. – Roland Jan 18 '21 at 18:22

1 Answers1

4

Note that if $k'/k$ is any finite separable extension of fields, then $k' \otimes_k \bar{k} \cong \bar{k}^{[k' : k]}$. So, given an extension of number fields $L/K$, a nonzero prime ideal $\mathfrak{p} \subseteq \mathcal{O}_K$ with residue field $k = \mathcal{O}_K/\mathfrak{p}$ is unramified in the extension $\mathcal{O}_L/\mathcal{O}_K$ if and only if the geometric fiber $\operatorname{Spec}(\mathcal{O}_L/\mathfrak{p} \otimes_{k} \bar{k})$ (that is, the base change of the fiber, which is a $k$-scheme, to the algebraic closure $\bar{k}$) has exactly $[L : K]$ closed points.

This exactly mirrors the situation for branched coverings of Riemann surfaces, where a branch point is exactly one where the fiber has fewer points than the degree of the covering map. The difference is that since we're dealing with non-algebraically-closed fields, we might have to extend the residue field in order to "see" the full size of the fiber.

From this perspective, here are geometric interpretations of inertia degree and ramification index of a prime $\mathfrak{b} \in \operatorname{Spec} \mathcal{O}_L$:

  • The inertia degree is the number of geometric points lying above $\mathfrak{b}$. In other words, the inertia degree tells you how many points a given prime splits into under extension of the base field.
  • The ramification index, conversely, is essentially the multiplicity with which points occur in the geometric fiber. So, for example, if $\mathfrak{p}$ is totally ramified, then the geometric fiber above $\mathfrak{p}$ will be of the form $\operatorname{Spec} A$, where $A$ is a $\bar{k}$-algebra that is $[L : K]$-dimensional as a $\bar{k}$-vector space, and we can think of this as a "point with multiplicity $[L : K]$".
Daniel Hast
  • 5,284
  • very good answer this is what i was looking for , just do you mean by the geomtric point lying above $\mathfrak{b}$ the number of point of intersection of the vertical line with the curve ,i,e for example (2) has inertia degree 1 ,and the vertical line from 2 to the curve intersects in one point is that what you mean ? – Aster Phoenix Jan 18 '21 at 21:38
  • do we have a formula or a method to compute the number of points in the fiber ? – Aster Phoenix Jan 18 '21 at 21:44
  • 1
    In your example of $\mathbb{Z}[i]$, the fiber above $(2)$ is $\newcommand{\Spec}{\operatorname{Spec}}\Spec \mathbb{Z}[i]/(2) \cong \Spec \mathbb{F}_2[x]/(x^2)$, so the geometric fiber is $\Spec \bar{\mathbb{F}}_2[x]/(x^2)$. Topologically, this consists of a single point, but the algebra of functions on it is $2$-dimensional, not one-dimensional, because of the nilpotent $x$ (corresponding to $1 + i$ in $\mathbb{Z}[i]$). So it's reasonable to informally think of this as a "point with multiplicity two". – Daniel Hast Jan 18 '21 at 21:48
  • 2
    How to actually compute the ramification index and inertia degree in practice is a whole other matter—my answer is just meant to give the abstract connection to geometry and some intuition about how it relates to the classical notion of ramification. I recommend Henri Cohen's "A Course in Computational Number Theory" for a detailed treatment of these computational questions. (Section 6.2 discusses algorithms to factor prime ideals of number fields.) – Daniel Hast Jan 18 '21 at 21:52
  • by a formula or a way i did't mean how to compute the factorization of prime ideals, i mean how to compute the number of point of the fiber , can you give a reference on that – Aster Phoenix Jan 18 '21 at 22:01
  • Computing the factorization into prime ideals is how you compute the number of points of the fiber. – Daniel Hast Jan 19 '21 at 00:35