Could exists a vector field on $\mathbb{S}^{2}$ with exactly $n$ zeroes?

Question

I just started to learn index theory of tangent vector fields. I'm aware of two examples on the sphere $\mathbb{S}^{2}$ with exactly one zero, which, which are $F(x,y) = (1-x^2-y^2)\partial x$ thought on $\mathbb{D}^2$ and then identify the boundary, I think it is

And one with two zeroes should be something like this

I was wondering, it exists a tangent vector field with $n$ zeroes on the sphere ? I thought that if I have $n$ zeroes (isolated), then thanks to the Poincarè-Hopf theorem the sum of the indices must be $\chi(\mathbb{S}^{2}) = 2$. I thought that some combination of $-1$ and $1$ and a final zero of index $2$ could do the job, but can this vector field actually exist? Something like defining a polynomial with $n$ distinct zeroes $p : \mathbb{C} \longmapsto \mathbb{C}$ can be extended to $\mathbb{S}^{2}$ to gain a tangent vector field on the sphere?

Thanks in advance, any help would be appreciated.

Answer 1

There is a useful smooth vector field $\mathcal V$ to know about on the plane, satisfying the following conditions

• $\mathcal V$ has one zero at $\mathcal O = (0,0)$.
• Except for $\mathcal O$, every vector in the vector field $\mathcal V$ is a positive multiple of $\frac{\partial}{\partial x}$.
• Outside of the ball of radius $r$ around the origin (where $r>0$ can be anything you want), the vector field $\mathcal V$ is equal to the constant vector field $\frac{\partial}{\partial x}$.

To construct $\mathcal V$, multiply $\frac{\partial}{\partial x}$ by a non-negative bump function on the plane, which has a unique zero at $\mathcal O$, and is equal to $1$ outside of the ball of radius $1$ around $\mathcal O$.

You can combine this example with known examples to get any finite number of zeroes (except zero zeroes, of course). For instance, start with your "one zero" example. Choose $k \ge 0$ points $p_i$, $1 \le i \le k$, distinct from that zero. There exist respective neighborhoods $U_i$ of these points, with disjoint closures, and diffeomorphisms $\phi_i : U_i \to B_i \subset \mathbb R^2$, where $B_i$ is an open ball, and $\phi_i(p_i) = \mathcal O$, and such that the vector field on $U_i$ is equal to the pullback of the vector field $\mathcal V$ with respect to $\phi_i$ and a choice of radius $r_i$, equal to half the radius of $B_i$. Now replace the given vector field on $B_i$ with the pulback of $\mathcal V$, which has the effect of adding an isolated zero at $p_i$. This gives a vector field on $S^2$ with $1+k$ zeroes.

Answer 2

Here's a more topological way to look at it, in terms of height functions and Morse theory. When $n$ is even, take a sphere that's reshaped to have $n/2$ local maxima, one global minimum, and $n/2-1$ saddle points (so it looks like a camel with $n/2$ humps, closed up at the bottom). (Then we have $\chi(S^2) = n/2-(n/2-1)+1 = 2$, as it should.) We can't make this work when $n$ is odd, since twice the number of saddle points must equal $n-2$.

At any rate, you get the vector field on the sphere by taking the gradient of the height function, i.e., by projecting a vertical unit vector (up or down doesn't matter) onto the tangent plane of the sphere at each point.

Answer 3

This is a somewhat boring answer, but I believe you can always construct such a vector field. Given a vector field on the plane, you can artificially put in zeros of index $0$ by multiplying it with a "dent" function, for example something like $1-e^{-r^2}$. Thus you can take the constant vector field, put in $n$ "dents" wherever you please, then stereographically wrap it back onto the sphere, which will give you an extra zero of index $2$ at the north pole.

Answer 4

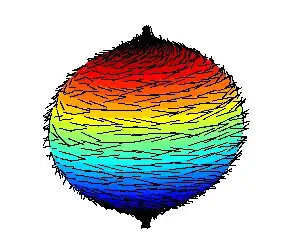
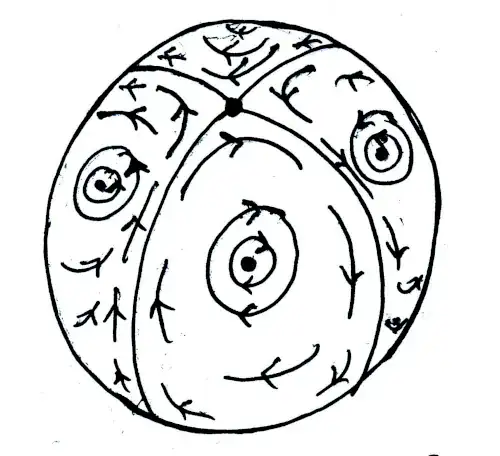
Complex polynomials won't work on their own, but a generalization can be made which allows one to produce an explicit formula (in stereographic coordinates) for any combination of indices which sum to $2$.

We can cover the Riemann sphere with two sets of opposite stereographic coordinates in the standard way, so that the transition function between them is $\tau(z)=1/z$, thinking of the tangent spaces $T_z\mathbb{C}$ as copies of $\mathbb{C}$ in the standard way, the differential of the transition function $d_z\tau:T_z\mathbb{C}\to T_{1/z}\mathbb{C}$ is just multiplication by $-1/z^2$.

We may treat a function $F:\mathbb{C}\to\mathbb{C}$ as a vector field in stereographic coordinates, and to see if it extends smoothly to the Riemann sphere, we can write its representative in the opposite coordinates, centered at infinity: $$ \widetilde{F}(z)=-z^2F(1/z) $$ We see that a complex polynomial of degree $>2$ will have a nonremovable singularity at infinity, but for degree $\le 2$ things behave as expected: each root has index equal to its algebreic multiplicity, and each polynomial of degree $d\in\{0,1\}$ has an additional zero of index $2-d$ at infinity. To get the other cases, we have to allow for negative indices; one way to do this is by complex conjugation.

Choose $a_1,\cdots,a_{n+2},b_1,\cdots,b_{n}\in\mathbb{C}\setminus\{0\}$, and define $$ F(z)=\frac{(z-a_1)\cdots(z-a_{n+2})(\bar{z}-b_1)\cdots(\bar{z}-b_n)}{1+|z|^{2n}} $$ This function is smooth on $\mathbb{C}$, and applying the transition function and doing a bit of algebra we obtain $$ \widetilde{F}(z)=-a_1\cdots a_{n+2}b_1\cdots b_n\frac{(z-1/a_1)\cdots(z-1/a_{n+2})(\bar{z}-1/b_1)\cdots(\bar{z}-1/b_n)}{1+|z|^{2n}} $$ And so $F$ extends smoothly to the Riemann sphere, and does not vanish at infinity. Additionally, the indices of the zeros of $F$ can be easily computed: for any zero $z_0\in\mathbb{C}$, the index of $z_0$ is the number of $a_i$ equal to $z_0$ minus the number of $b_i$ equal to $z_0$. This can be seen by first showing that the index of the vector field $V(z)=z^p\bar{z^q}$ is $p-q$ using polar decomposition, and looking at $F(z_0+z)$ in a small neighborhood around the origin.

Using this functional form, to obtain zeros of indices $I_1,I_2,\cdots,I_m\in\mathbb{Z}$ at distinct coordinates $z_1,\cdots,z_m\in\mathbb{C}$ we can choose positive integers $r_1,\cdots,r_m,s_1,\cdots s_n\in\mathbb{N}$ such that $r_i-s_i=I_i$ and then choose $a_1,\cdots,a_{n+2}$ to contain $r_i$ copies of each $z_i$ and $b_1,\cdots,b_n$ to contain $s_i$ copies of each $z_i$.

Answer 5

Yes, and it is possible to choose the indices of the zeros freely as long as the sum is $2$. The first part of this answer is a slight variation of Kajelad's.

Let $n_1,\dots,n_k > 0$ with $n_1+\cdots+n_k \geq 2$ be the positive multiplicities. The polynomial $(z-1)^{n_1}\cdots(z-k)^{n_k}$ gives a vector field on $\mathbb{C}$ that looks like $z^{n_1+\cdots+n_k}$ when $z$ is big. Let's compute what this field looks like around $∞$ on the Riemann sphere. We apply the change of charts given by $z \mapsto 1/z$, so we precompose our field by this function and divide by $(1/z)' = -1/z^2$. This gives $(1/z)^{n_1+\cdots+n_k-2}$. The $2$ of the Euler characteristic appears here. There is a pole at $0$ but we can transform it to a zero instead by inverting the norm of the field, with a smooth transition. It gives $\overline{z}^{n_1+\cdots+n_k-2}$. The $\overline{z}$ means that the multiplicity is negative instead of positive but except from that, we are in the same situation as before and we can apply the same technique to separate this zero into as much zeroes of negative multiplicities as we want.

We can add zeroes of index $0$ by multiplication with a real field vanishing at the desired points, as in the answer of Elliot Yu.

---

Here is an example of a field with four zeroes of multiplicities $1$ (we only see three of them) and two zeroes of multiplicities $-1$ (we only see one of them).

More generally, if you have a finite set of closed loops with self-intersections on the sphere (here, two perpendicular circles separating the sphere into four quarters), then you can build a field by placing one zero of multiplicity $1$ into each of the delimited region and a zero of multiplicity $-1$ at each intersection point of the loops. Each zero of multiplicity $1$ has a "typhoon" going around it as in the drawing above and the directions of these typhoons alternate as we change of region. To see that it always works, we can do by recursion on the number of self-intersections: remove an intersection point by merging two opposite regions.

For instance, a loop drawing an 8 will produce three zeroes of multiplicities $1$ and one zero of multiplicity $-1$.

Look also at this old video of Vi Hart: https://www.youtube.com/watch/heKK95DAKms When she colors the regions, the black ones are those oriented in one direction and the white ones are those oriented in the other direction.

I don't know how this reverses nor the general theory behind all of this, so if someone knows the keywords, I'm interested.