How few $(42^\circ,60^\circ,78^\circ)$ triangles can an equilateral triangle be divided into?

Question

This is the parallel question to this other post with many answers already, in the sense that the $(42^\circ,60^\circ,78^\circ)$-similar triangles form the only non-trivial rational-angle tiling of the equilateral triangle (and the regular hexagon), modulo a real conjugation of the coordinate field (a subfield of $\mathbf{Q}(\zeta_{60})$) which transforms between $(42^\circ,60^\circ,78^\circ)$-similar triangles and $(6^\circ,60^\circ,114^\circ)$-similar triangles. (Reference: M. Laczkovich's Tilings of triangles.)

My attempt has been the following:

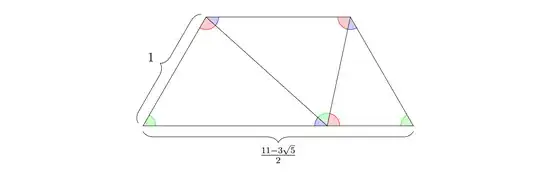
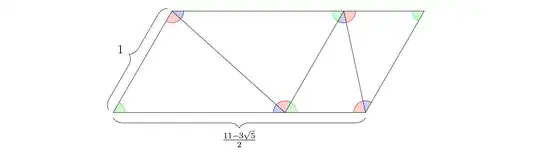
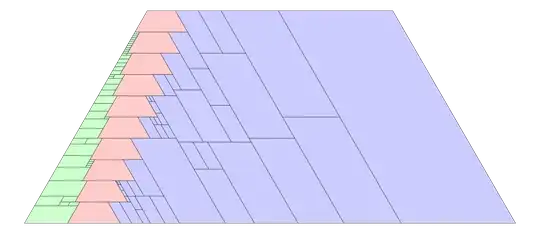
Since $\sin(42^\circ)$ and $\sin(78^\circ)$ have nested radicals, I tried to get rid of them by restricting my basic tiling units to only the $60^\circ$-angled isosceles trapezoids and parallelograms that are a single row of the triangular tiles. They have shorter-base-to-leg ratios of the form $$m\cdot\frac{9-3\sqrt{5}}{2}+n\cdot\frac{11-3\sqrt{5}}{2}\quad\left(m,n\ge 0\right)$$ which are automatically algebraic integers. Any potential tiling of the equilateral triangle from these quadrilateral units corresponds to some integer polynomial relation of the above algebraics, whose polynomial degree correlates with the number of quadrilateral pieces in the tiling.

Unfortunately all the above algebraics have large norms, so a blind search for the desired polynomial is out of the question, and I had to reduce the pieces' proportions again to the rationals. I was able to find a $60^\circ$-angled isosceles trapezoid with shorter-base-to-leg ratio of $10$ using $79$ tiles, and a $60^\circ$-angled parallelogram with neighboring sides' ratio of $11$ using $80$ tiles. Thus a few more tiles produce a $60^\circ$-angled rhombus, and another few more tiles produce a $60^\circ$-angled isosceles trapezoid with shorter-base-to-leg ratio $1$, three of which tile an equilateral triangle, using a total of $121\,170$ triangular tiles. While I was at it, I found this less related post that might reduce my number of tiles to a bit below a hundred thousand.

Meanwhile, I also did a quick computer search through some conceptually simple configurations that attempt to tile the equilateral triangle using less than about $50$ tiles, and I found nothing at all.

I get this feeling that about a hundred thousand tiles is not the optimal amount for such a tiling, so I'm asking to see if people have better ideas. I'm unable to provide cash incentive as the parallel post did, but anyone who tries this puzzle will sure have my gratitude.

---

Edit suggested by RavenclawPrefect:

To get to the quadrilateral tiling units that I used, the first thing is to de-nest the radicals as I mentioned above. As $\mathbf{Q}(\zeta_{60})$ is Galois over $\mathbf{Q}(\sqrt{3})$ (the base field here should not be $\mathbf{Q}$ but instead the coordinate field of the equilateral triangle), if we can geometrically construct any length $\ell$ (or techinically, ratio $\ell$), such that when we perform the same geometric construction but with all the $42^\circ$ angles and $78^\circ$ angles swapped with each other, we still provably construct the same $\ell$, then it must hold that $\ell\in\mathbf{Q}(\sqrt{5})$, so that $\ell$ doesn't contain any nested radicals.

There were a couple of ideas on what $\ell$ should specifically be, most of them parallel ideas that can all be found in the parallel question for the square. I settled on the above $\mathbf{Q}(\sqrt{5})$-quadrilaterals (the ones that are a single row of triangular tiles) because they had the smallest numerator norms among others. As a non-example, there was a double-decker idea using $9$ tiles that resulted in a trapezoid with ratio a rational multiple of $889-321\sqrt{5}$, yuck. There were also some non-triviality in which way the triangles should be oriented when being put into a single row, but some more calculation showed that the above $(m,n)$ form are all we really get. More precisely, a trapezoid also can't have $m=0$, and a parallelogram also can't have $n=0$.

After all that work, the rest has really been a matter of trial-and-error. Among all the $(m,n)$ form, I picked a parallelogram with the smallest norm, which is an $(m,n)=(0,1)$ parallelogram with $4$ tiles, and rotated it so that it becomes a $\frac{11+3\sqrt{5}}{38}$-parallelogram. Then $19$ of those make a $\frac{11+3\sqrt{5}}{2}$-parallelogram with $76$ tiles, and obviously I combined it to a $(1,0)$-trapezoid and a $(0,1)$-parallelogram to get to the rational quadrilaterals.

So the process was more like "I frankly don't know what else to do" rather than "I see potential simplifications but I don't know the optimum". It's also why I'm seeking for completely new ideas (see above) that aren't found in the parallel question about the square.

RavenclawPrefect also asked a well-motivated question for if the same tiling could be performed but with congruent tiles. M. Laczkovich proved this is impossible in a subsequent paper Tilings of Convex Polygons with Congruent Triangles.

Answer 1

I'm posting a new answer to this question, because the techniques I'm using differ substantially from the previous answer and it was already getting quite long. (Much of this answer was written prior to Anders' excellent answer, so it retreads some ground there.)

Edit: This answer in turn has been updated many, many times with improved constructions - feel free to peruse the edit history to see my earlier attempts.

To start with, I'd like to better flesh out the constructions outlined in the OP, as I found looking at these diagrams helpful. Define a parallelogram of ratio $r$ as one with sides $1,r,1,r$ in cyclic order, and a trapezoid of ratio $r$ as one with sides $1,r,1,r+1$ in cyclic order. (I'll implicitly assume that everything has $60^\circ$ and $120^\circ$ angles and that all trapezoids are isosceles unless otherwise stated.)

Here is an isosceles trapezoid of ratio $\frac{9-3\sqrt{5}}2$ made from three $\color{blue}{42}-\color{green}{60}-\color{red}{78}$ triangles:

Here is a parallelogram of a ratio $1$ larger (so with the same base) made from four such triangles:

(Note that it is not given by adding a triangle to the previous construction! The bottom three points are in the same location, though.)

As Edward H observes, we can actually extend either of the two parallelograms above by inserting a non-$60$-degree parallelogram in between an edge where only red and blue angles meet; this lets us spend $2$ more triangles to create trapezoids and parallelograms of ratios $\frac{9-3\sqrt{5}}{2}$ more.

Now, some observations:

• A parallelogram of ratio $r$ is also a parallelogram of ratio $1/r$: just turn it on its side!

• Given two parallelograms of ratios $r,s$, we can put them together to get a parallelogram of ratio $r+s$.

• Given a trapezoid of ratio $r$ and a parallelogram of ratio $s$, we can put them together to get a trapezoid of ratio $r+s$.

• Given two trapezoids of ratios $r,s$, we can turn one of them upside down and then put them together to get a parallelogram of ratio $r+s+1$ (because the top side is one unit shorter than the bottom side).

• Given two trapezoids of ratios $r,s$, we can put one on top of another to get a trapezoid of ratio $rs/(r+s+1)$.

This gives us an obvious path forward: start with our two basic trapezoid and parallelogram solutions (plus their extensions), then combine them in the above ways looking for small tilings of nice rational-ratio trapezoids and parallelograms until we find a set we can nicely fill an equilateral triangle with.

I wrote up some code to perform exact computations with elements of $\mathbb{Q}[\sqrt{5}]$, and started storing all of the trapezoids and parallelograms one can make with up to around $90$ triangles, but bounding the size of the rational numbers involved to prevent the search space from getting too out of hand. (If I have a parallelogram of ratio $1173/292-46\sqrt{5}/377$, I'm probably not going to end up needing it.)

This alone doesn't turn up very many rational-ratio shapes, so I ran a second script that checked amongst all of the shapes generated in the previous iteration for those whose irrational parts were the negatives of each other, and combined them into new, rational-ratio shapes.

The results of this search included many interesting constructions, including Anders Kaseorg's 72-triangle solution for a parallelogram of unit ratio, but for our purposes we can focus on three of them: an $89$-tile trapezoid of ratio $3$, a $97$-tile trapezoid of ratio $2$, and a $113$-tile trapezoid of ratio $3/2$, shown below from top to bottom:

If we place the ratio-2 trapezoid on top of the ratio-3 trapezoid, we obtain a trapezoid of ratio $1$ using $186$ triangles:

Triplicating this would let us obtain an equilateral triangle with $558$ triangles, but we can do better using the ratio-$3/2$ trapezoid. Observe that three trapezoids form an equilateral triangle if and only if their ratios multiply to $1$. So, by stacking a ratio-$2$ trapezoid on a ratio-$3$ trapezoid, we obtain a ratio $2/3$ trapezoid, which combined with the ratio-$3/2$ trapezoid and the ratio-$1$ trapezoid forms an equilateral triangle.

Here is an image of the full (asymmetric!) construction, with all $(89+97)+(97+113)+113=\textbf{509}$ triangles in one piece:

Answer 2

From the OP, I'm using the fact that we can use $79$ triangles to tile a trapezoid with side lengths $11,1,10,1$ and angles of $60$ and $120$ degrees, as well as the parallelogram with side lengths $1$ and $11$ with $80$ triangles. This means that we can tile a "diamond" (the union of two edge-connected equilateral triangles) using $11\cdot80=880$ triangles.

We can then fit all these pieces onto a triangular grid: the trapezoid takes up $21$ triangles, the skinny parallelogram $22$, and the diamond-shaped region just $2$ (but at a great cost). Of course, any of them can be scaled up by some integer factor and still lie on the grid.

Using some code I wrote to solve tiling problems plus some manual modifications, I have found the following packing of an isosceles trapezoid with base-to-leg ratio $1$ (in this case, scaled up on the triangular grid by a factor of $12$ in each dimension):

It uses $12$ trapezoids and $19$ diamonds (the latter of varying sizes). Thus, tiling an equilateral triangle with three copies of this shape will use $3\cdot(12\cdot79+19\cdot880)=\textbf{53004}$ tiles.

Edit by nickgard:
A smaller tiling of the same trapezoid using $10$ long trapezoids and $12$ diamonds.
$3\cdot(10\cdot79+12\cdot880)=\textbf{34050}$ tiles.

(End of edit)

EDIT (RavenclawPrefect): I've found some improved ways to tile parallelograms, which can be used along with nickgard's solution to reduce the number further.

Here is a tiling of a $1\times 2$ parallelogram with seven $1\times 11$ parallelograms (contrast with the $22$ it would take by joining two rhombi together):

In general, one can tile a $1\times n$ parallelogram for $n=1,\ldots,9$ with $11,7,6,6,6,6,6,6,7$ skinny parallelograms; these values arise from taking a tiling of an $11\times n$ rectangle by squares (see A219158 on OEIS) and applying an appropriate affine transformation.

For the $1\times 7$, using $6$ skinny parallelograms gives us $6\cdot 80$, but we can also use $6$ trapezoids as described in Edward H's comment on this answer for $6\cdot 79$ tiles, which offers a slight improvement.

Using these more efficient packings, I can fill in the "staircase" shape in nickgard's answer as follows:

This uses a total of $4874$ tiles in the staircase, $4874+10\cdot79 = 5664$ in the trapezoid, and $\textbf{16992}$ in the triangle.

Edit 2 (RavenclawPrefect): After lots of fiddling around with decomposing the "staircase" shape into nice axis-aligned parallelograms, I realized that I could just apply an affine transformation, turning the whole staircase into a very tall polyomino of size ${10\choose 2}\cdot 11=495$ with "steps" of height $11$, and try to tile the resulting thing with squares directly.

This resulted in a substantial improvement, giving a tiling with $46$ squares (hence, $1\times 11$ parallelograms once transformed back); the resulting image would not embed well due to its height, but I have uploaded it to imgur here. Update: I have slightly improved this tiling to a $45$-square solution, seen here.

This results in $3\cdot(45\cdot80+10\cdot79)=\textbf{13170}$ tiles.

Ways this might be improved:

• Trying for a better packing of this $495$-omino by squares - my search was not exhaustive, and I think there's at least a $30\%$ chance it can be tiled more efficiently.

• Finding a better packing of some trapezoid or equilateral triangle with these same methods - I certainly haven't optimized things as much as I could.

• Finding a more efficient "base" packing of either of the seed shapes used in this tiling, or generating new relatively simple polyiamonds that can be efficiently tiled with $42-60-78$ triangles.

Answer 3

Here’s a trapezoid of ratio $1$ tiled by $195$ triangles, found in a brute-force search. Using three of these to build an equilateral triangle takes $3 \cdot 195 = \mathbf{585}$ triangles.

Old answer

This basic $60^\circ$ trapezoid of ratio $\frac{9 - 3\sqrt 5}{2}$ uses three triangles, and this basic $60^\circ$ parallelogram of ratio $\frac{11 - 3\sqrt 5}{2}$ uses four triangles:

Any number $r \in \mathbb Q[\sqrt 5]$ can be decomposed as $r = \frac{11 - 3\sqrt 5}{2}u + \frac{2}{11 - 3\sqrt 5}v$ with $u, v \in \mathbb Q$. If $u, v \ge 0$, then we can tile a parallelogram of ratio $r$ using basic parallelograms by combining affine transformations of the tilings of rectangles of ratios $u$ and $v$ using squares. For example, here’s a 72-triangle parallelogram of ratio $1 = \frac{11 - 3\sqrt 5}{2}\cdot\frac{1}{11} + \frac{2}{11 - 3\sqrt 5}\cdot\frac{19}{11}$, derived from square tilings of $1 × 11$ and $19 × 11$ rectangles.

Using this idea in a version of the “staircase” construction yields much more efficient tilings of the trapezoid of ratio $1$. Here’s one with $45 \cdot 4 + 10 \cdot 3 + 44 \cdot 4 = 386$ triangles. (I’m now using a dynamic programming algorithm that tiles the green region and the blue region each in one pass rather than slicing them into parallelograms. For clarity, divisions of basic trapezoids/parallelograms into three/four triangles are not pictured.)

Using three of these to build an equilateral triangle takes $3 \cdot 386 = \mathbf{1158}$ triangles.

Probably a yet more efficient tiling could be constructed by cutting a small number of basic trapezoids out of the equilateral triangle more or less arbitrarily until a single parallelogram remains, solving for its ratio $r \in \mathbb Q[\sqrt 5]$, and applying the above rectangle-tiling construction once. Finding a way to do this such that $u, v \ge 0$ has been trickier than I expected though.