5

I am solving the problems in Michael Spivak's Calculus book. In the Prologue chapter, there is the following problem: $$x + 3^x < 4$$ I can solve this using graphical means, but not analytically. Is it possible to do the latter?

I can arrive at the solution as follows:

$$3^x < 4 - x$$

$$x < \log_3 (4-x)$$

I then draw the graphs of the functions $\log_3 (4-x)$ and $x$, and I can determine that $x$ needs to be smaller than 1 to be smaller than the $\log_3 (4-x)$.

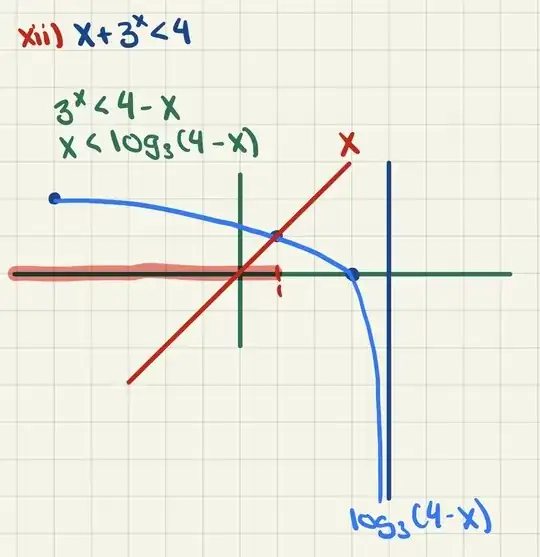
enter image description here

How do I solve this purely analytically?

IV_
  • 7,902
xoux
  • 5,079

3 Answers3

2

$$x+3^x-4=0$$

1.) Solution as series

To solve the equation analytically as a series, you can use Lagrange inversion.

2.) No solution with elementary inverses

The equation is a zeroing equation of an elementary function.

Powers with irrational exponents are transcendental functions. Therefore the equation isn't an algebraic equation, it's a transcendental equation:

$$x+e^{\ln(3)x}-4=0$$

Because $x+e^{\ln(3)x}-4$ is a polynomial of two algebraically independent monomials simultaneously ($x,e^{\ln(3)x}$), the function $\mathbb{R}\to\mathbb{R}, x\mapsto x+e^{\ln(3)x}-4$ seems to have no elementary partial inverse. For the same reason, we cannot rearrange the equation by applying only finite numbers of only elementary functions (elementary operations) which we can read from the equation.
But we can see if we can guess solutions.

3.) Solution in closed form with Lambert W

The equation is solvable by applying Lambert W. By some simple rearrangings, we can bring the equation into a form that is solvable by Lambert W.
The only real solution is: $$x=\frac{4\ln(3)-W(81\ln(3))}{\ln(3)}.$$

That's equal to $1$, but I don't know the methods to show this.

IV_
  • 7,902
1

$x+3^{x}$ is a continuous strictly increasing function. Hence $\{x: x+3^{x}<4\}=(-\infty, t)$ where $t$ is the unique real number $t$ such that $t+3^{t}=4$. Note that $t=1$!

Kavi Rama Murthy
  • 359,332
  • How do I solve for t? – xoux Dec 30 '20 at 05:11
  • @evianpring $t=1$ solves it and there is only one possible solution for this equation. – Kavi Rama Murthy Dec 30 '20 at 05:12
  • 2
    Yes, of course. But I’m wondering if there is some analytical operation that I can do to arrive at t = 1. Is it simply the case that I must guess the number (even though in this case it is easy to do so)? – xoux Dec 30 '20 at 05:13
  • 3
    "But I’m wondering if there is some analytical operation" : Meta-Cheating, I would blindly speculate that no there is not, for three reasons: [1] If there were such an operation, the problem would have been re-structured to force you to find the operation, rather than yielding to the obvious guess of equality at $x = 1$ [2] No one in mathSE has stepped up to say : Yes, here is how you do it. and [3] Spivak (presumably) presented the problem with no specific prior training on how to analytically attack such problems. ...see next comment. – user2661923 Dec 30 '20 at 05:22
  • 3
    This all begs the question, what was the point of the problem? I would speculate, that having found equality when $x=1$, you were supposed to recognize that for $x > 1$, the function is continuous and strictly increasing. – user2661923 Dec 30 '20 at 05:25
  • 3
    The point of this problem seems to be to check if you can recognize the increasing nature of the function $x+3^{x}$ (not from the graph, but using Calculus) and not solve an equation. @evianpring – Kavi Rama Murthy Dec 30 '20 at 05:28
  • IMO this part of the exercise (1-4.(xii), 3rd ed.) should not have been included in the chapter. This also goes for the two preceding parts (x) and (xi), each of which similarly involve expressions beyond the scope of what Spivak carefully lays out in the chapter ($\sqrt[3]{2}$ and $2^x$, respectively.) – Ben Dec 30 '20 at 15:42
  • 1
    While it's fair to assume readers would have previous familiarity with these things and be able to guess the answer, these parts are at odds with the rigour Spivak's trying to encourage elsewhere. There are some mistakes and errors in the book. IMO these 3 parts of problem 1-4 should not have been included. – Ben Dec 30 '20 at 15:46
  • 1
    Note this exercise comes before the concept of functions is introduced. The reader is absolutely not expected to make arguments that use continuity or strickly increasing functions. – Ben Dec 30 '20 at 15:56
  • 1
    All that said, don't let this put you off @evianpring. Keep going! The rewards in the book far outweigh the few hiccups. I suggest keeping a list of suspected errors and mistakes you find during your reading. – Ben Dec 30 '20 at 16:15
0

As @IV_ writes (in solution 3), standard application of Lambert's W function gives the solution:

$$x = \frac{4 \log (3)-W(81 \log (3))}{\log (3)}$$

Note that $W(81 \log (3)) = \log (27)$, so the full solution gives $x=1$, which can be easily confirmed.

David G. Stork
  • 30,409