4

This year, there was published a closed-form solution to the Goat Problem. The problem seeks the radius of a circle (teal) with center on the edge of a unit circle (green) such that the first circle overlaps half of the unit circle.

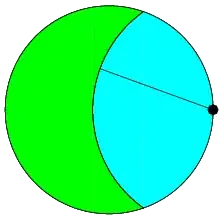
Image from https://mathworld.wolfram.com/GoatProblem.html

The solution given is

$$r=2\cos\left(\frac{{\Large\oint}_{\large|z-3\pi/8|=\pi/4}{\Large\frac{z}{\sin{z}-z\cos{z}-\pi/2}}dz}{{\Large\oint}_{\large|z-3\pi/8|=\pi/4}{\Large\frac{2}{\sin{z}-z\cos{z}-\pi/2}}dz}\right)= 1.15872847\dots$$

Can we simplify this further? I noticed that the divided integrals look like a center of mass formula. I tried converting the contour integrals into real integrals, but didn't get very far. I don't have much experience with complex integration. Also, I don't have access to the paper, but maybe there is some information there that can help us.

tyobrien
  • 3,667
  • 10
    I wouldn't call that a "closed form", because you can evaluate the integrals only numerically. It's just residues the other way round, and you could write it with only one integral, obviously. –  Dec 27 '20 at 07:27
  • 1
    Indeed, to compute the integral you need to find the poles, which are the solutions of the transcendental equation $\sin z-z\cos z=\frac\pi2$. Just stalling. –  Sep 02 '24 at 09:15
  • FWIW, simple iteration on the angle in the transcendental equation converges quadratically. https://sagecell.sagemath.org/?z=eJxNjkEOgyAQRfec4qfdQGM1smqbkHTXYxi0qBMpEOD%2DacRqOsv3%5Fp%2DZM15eZ4Toe2s%2D7Ekum6iHzN5mRMd7ykm18iYeDAC0DbOGguNtfa%2DwWlHEHKjgQI3859b7kKAKqXvKnTVuyjMXuEKWxOgjCOQQtZsML4XftXUWKCRyvFxeW3OgQ%2D7v6MEnvqDZgDh8iOQyp2rnRUQoSFywdrYFDeTW2fKneKoQBfsCcetNFg==&lang=sage – PM 2Ring Sep 21 '24 at 07:53

2 Answers2

2

Because there is implied some complex trigonometric function algebra, use Mathematica

Manipulate[With[{},
  RegionPlot[{(x - 1)^2 + y^2 < 1 , x^2 + y^2 < R^2 , 
                     x^2 + y^2 < 1}, {x, 0, 2}, {y, -1, 1},
 Epilog -> {
 {Arrow[{{0, 0}, {R, 0}}], 
  Arrow[{{0, 0}, R {R/2, Sqrt[1 - R^2/4]}} ]},
 {Arrow[{{R, 0}, R {R/2, Sqrt[1 - R^2/4]}}]}, {Text[
   Rationalize[
     NIntegrate[
      Boole[(x - 1)^2 + y^2 < 1 && x^2 + y^2 < R^2 ]/\[Pi], 
        {x, 0,2}, {y, -1, 1}], 1/100] *\[Pi], {R/2, 1/4}]}}]],
  {{R, 1.16}, 0, 2}, ControlPlacement -> Top]

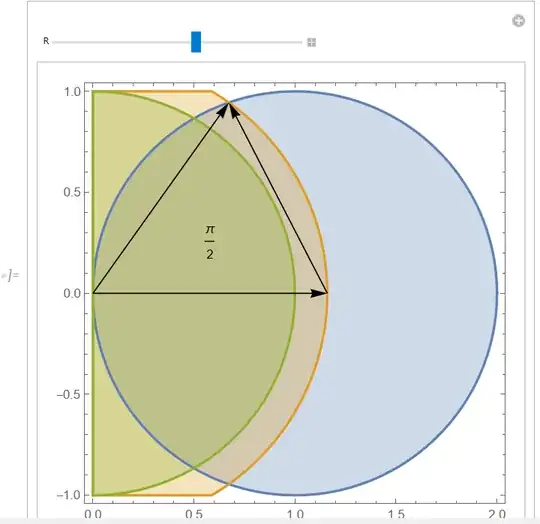
Goat Gazing Area

Graphics[{{Thickness[0.01], Blue, Circle[{1, 0}, 1]}, 
          {Thickness[0.01], Red, Circle[{0, 0}, 1.3, {-\[Pi]/3, \[Pi]/3}]},
          {Opacity[0.5], 
           Array[(Circle[{0, 0}, #1/6, Cos[#/9] {-\[Pi]/2, \[Pi]/2}] &), 9]},
        RegionPlot[(x - 1)^2 + y^2 < 1 && x^2 + y^2 < 1.7 , 
           {x, 0,  2}, {y, -1, 1}][[1]],
        {Green, Thickness[0.02], 
        Line[ 
        {x0 = {0, 0}, x1 = {1.3 Cos[0.85], 0}, x2 = 1.3 {Cos[0.85], Sin[0.85]}, 
         {0, 0}}]},
         {Black, Arrow@{{ x0, x1}, {x1, x2}, {x0, x2}}},  
       Text["r", 1/2 {1, 1}], Text["\[Alpha]", {0.2, 0.1}],
       Text["r cos \[Phi]", {0.4, -0.05}], Text["r sin \[Phi]", {1, 0.5}]},
       PlotRange -> {{0, 2}, All}]

The two circles have the point of intersection at

$$(a\cos \phi - 1)^2 + a^2 (1 - \cos^2 \phi) \ = \ 1 \quad \leftarrow \quad \phi= \cos^{-1}\left(\frac{r}{2}\right)$$

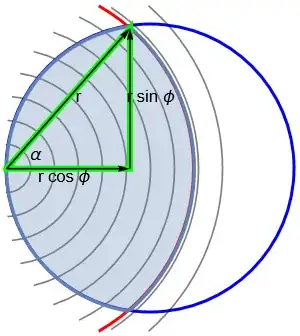
Grazin Area Polar

So we have

$$\begin{align}&\text{GrazingArea}(R) \ = \ \int _0^R\int _{-\sin ^{-1}\left(\sqrt{1-\frac{r^2}{4}}\right)}^{\sin ^{-1}\left(\sqrt{1-\frac{r^2}{4}}\right)} d\phi\ \ r dr \ \\& = \ \ \frac{1}{2} R \left(\pi R-\sqrt{4-R^2}\right)-\left(R^2-2\right) \sin ^{-1}\left(\frac{R}{2}\right) \end{align}$$

The result is showing that the non grazed area is simple

$$\begin{align}&\text{NonGrazingArea}(R) \ = \ \int _R^2\int _{-\sin ^{-1}\left(\sqrt{1-\frac{r^2}{4}}\right)}^{\sin ^{-1}\left(\sqrt{1-\frac{r^2}{4}}\right)}rd\phi dr \ \ \\& = \ \ \frac{1}{2} R \sqrt{4-R^2}-\left(R^2-2\right) \cos ^{-1}\left(\frac{R}{2}\right) \end{align}$$

The numerical solution

  fr = R /. 
      FindRoot[NonGrazingAreal[R] - \[Pi]/2, {R, 1}, 
            WorkingPrecision -> 128, AccuracyGoal -> 128]

1.15872847301812151782823350993350914968829226649209651182069588482066
       98025591960931993216107308604381759674951803405182901392509

is surely transcendental

Partition[ContinuedFraction[fr],16]

$$\left( \begin{array}{cccccccccccccccc} 1 & 6 & 3 & 3 & 149 & 6 & 5 & 1 & 5 & 16 & 61 & 1 & 4 & 58 & 1 & 2 \\ 2 & 4 & 1 & 7 & 23 & 3 & 1 & 1 & 3 & 20 & 1 & 8 & 1 & 2 & 8 & 2 \\ 2 & 1 & 2 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 5 & 1 & 2 & 1 & 1 & 1 \\ 6 & 1 & 285 & 2 & 1 & 1 & 1 & 4 & 1 & 1 & 1 & 17 & 2 & 5 & 1 & 2 \\ 6 & 3 & 1 & 1 & 1 & 5 & 1 & 4 & 5 & 2 & 9 & 1 & 1 & 7 & 1 & 2 \\ 1 & 2 & 3 & 4 & 5 & 1 & 1 & 4 & 1 & 5 & 1 & 12 & 2 & 2 & 1 & 2 \\ 5 & 91 & 4 & 2 & 1 & 3 & 2 & 2 & 1 & 2 & 7 & 3 & 1 & 9 & 2 & 2 \\ \end{array} \right)$$

Roland F
  • 5,122
2

Assuming that you isolated a simple root $z_0$ of the equation $f(z)=0$ in a domain inside a contour $\mathcal C$ (such as a circle that contains it), that root can be obtained as

$$\dfrac{\displaystyle\oint_{\mathcal C}\dfrac z{f(z)}dz}{\displaystyle\oint_{\mathcal C}\dfrac 1{f(z)}dz}.$$

Indeed, by the residue theorem, this is the ratio

$$\dfrac{\lim_{z\to z_0}\dfrac{z(z-z_0)}{f(z)}}{\lim_{z\to z_0}\dfrac{z-z_0}{f(z)}}=z_0.$$

This explains the "closed form" solution, and shows that it does not help unless you are able to compute the integrals directly.

So the paper made a non-discovery.