This question is related to the potential possibilities of classification of divergent integrals more precisely than just "divergent to infinity" and the like. Improper divergent integrals can have many distinguishing properties, like germ at infinity, rate of grow and regularized value. A separate question is whether we can talk about equivalence (in whatever sense) of integrals divergent at infinity and those divergent at a singularity or pole.
For instance, formally applying the Laplace transform we can establish the following formal relations (for $n>0$):
$$\int_0^1 x^{-1+n} dx=\int_1^\infty n!x^{-1-n}dx$$
and
$$\int_1^\infty x^{-1+n} dx=\int_0^1 n!x^{-1-n}dx$$
This works for convergent integrals:
$$\int_0^1 dx=\int_1^\infty \frac1{x^2}dx=1$$
If generalized to divergent integrals, it also seems to work well, the equality
$$\int_1^\infty dx=\int_0^1 \frac1{x^2}dx$$
seems to be supported well by the hyperfunction theory.
But with $n=0$ we have (in the both formulas):
$$\int_0^1 \frac1x dx=\int_1^\infty \frac1x dx$$
This looks counter-intuitive at the first glance, as the figures under the integrals are identical up to a reflection relative the $y=x$ axis, except the first one has an additional $1\times 1$ square.
Of course, since the integrals are divergent, it should not be an obstacle to the identity (as the positions of the figures and the limits of integration are different). The both integrals are regularizable to the value $0$.
So, I wonder, if there is any intuition or example from other fields or mathematics or physics where these integrals demonstrate equivalence in a more strict sense than being both divergent to infinity?
For instance, from geometry or probability theory.
UPDATE
It seems, the equality should not hold, and the more correct one would be $$\int_0^1 \frac1x dx=\gamma+\int_1^\infty \frac1x dx$$

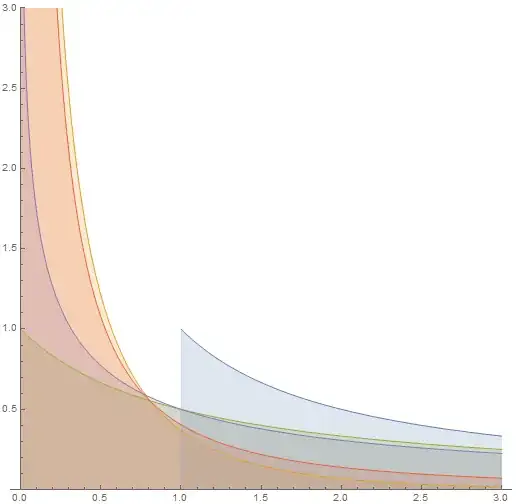
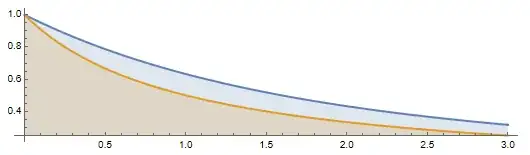
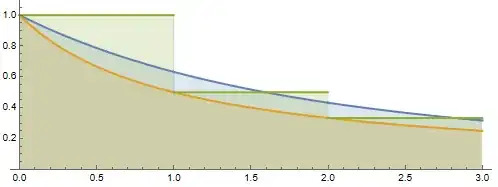
$$\int_{1/N}^1 \frac{dx}{x} = \int_{1}^N \frac{dx}{x} = \ln N,$$ where $N \gg 1$. Not sure if this is what you are looking for
– mikefallopian Dec 24 '20 at 02:48