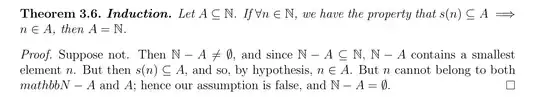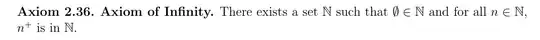2

enter image description here

The above proof is from an introductory paper on ordinals. I'm confused by the proof since it seems to assume that every subset of $\mathbb{N}$ has a smallest element, which is something the paper doesn't prove. I went online looking for proofs that $\mathbb{N}$ is well-ordered, but all the ones I've found use induction in one way or another, so I wonder how one could prove that $\mathbb{N}$ is well-ordered without appealing to induction.

In case it is relevant, the paper defines $\mathbb{N}$ by means of the Axiom of Infinity:

enter image description here

Sam
  • 5,208

1 Answers1

1

You can't really do that.

For a partial order $(P,<)$ we say that $P$ has "capacity for induction"1 if whenever $A\subseteq P$ is such that all the minimal elements are in $A$, and whenever $a\in P$ is such that $\{x\in A\mid x<a\}\subseteq A$, then $a\in A$, then $A=P$.

Theorem. $(P,<)$ has capacity for induction if and only if for every non-empty $A\subseteq P$, there is a minimal element in $A$ (relative to the restricted order).

In other words, capacity for induction is equivalent to being well-founded.

Corollary. If a $P$ is a linear order, then it has the capacity for induction if and only if it is well-ordered.

This means that we can't prove that $\Bbb N$ has the capacity for induction without using the fact that it is well-ordered. Luckily we are not working with the Peano axioms, we are working in $\sf ZF$, where we can prove the fact that our set $\Bbb N$ is in fact well-ordered without appealing to induction principles internal to $\Bbb N$.

Finally, as a small side note, the paper you're reading should state that $\Bbb N$ is not just "a set" with these properties, but in fact the smallest such set.

  1. This is an ad-hoc term, but the definition is not ad-hoc.
Asaf Karagila
  • 405,794
  • Yes, masiewpao's comment shows how $\mathbb{N}$ being well-ordered is equivalent to $\mathbb{N}$ having what you call 'capacity for induction'. How could one prove that $\mathbb{N}$ is well-ordered in ZF without appealing to induction though? – Sam Dec 22 '20 at 14:59
  • 1
    Prove that $\in$ is a linear ordering on $\Bbb N$ and then use the fact that $\in$ is well-founded. (Also, looking briefly at this note, it is not a very high quality note for learning about ordinals and cardinals. Why are you using this one specifically? As a general rule of thumb, it's good to learn about set theory from someone who's research is in set theory, not someone who did a summer study on the topic and is in fact not a mathematician to begin with.) – Asaf Karagila Dec 22 '20 at 15:04
  • Regarding "capacity for induction", I like the concept and terminology of "inductive set" which is used in Fitzpatrick's Advanced Calculus, albeit in the limited context of subsets of the real numbers, and in a slightly different way than your definition, but yet it captures kind of the same flavor as your definition. – Lee Mosher Dec 22 '20 at 15:16
  • @AsafKaragila Oh no reason really, I believe it was the first one I found online and decided to go with it. – Sam Dec 22 '20 at 15:27
  • @Lee: But inductive means something else, normally it means "contains 0 and closed under successor". – Asaf Karagila Dec 22 '20 at 15:43
  • Yeah, but I thought the "contains $0$" was similar to your requirement that all minimal elements are in $A$. Anyway, just a thought. – Lee Mosher Dec 22 '20 at 16:18
  • @Lee: It's a little similar, yes. Then you'd say that every inductive subset equals the whole poset. I wanted a property that terms the whole poset, not just subsets of it. – Asaf Karagila Dec 22 '20 at 16:58
  • @Leo: I see. If your goal is to study set theory, I suggest that you use one of the more traditional books or lecture notes. (I have lecture notes on my website, but those might be hard since they were aimed at my students who had previously taken a class with the very basics of set theory. Enderton is pretty good as far as set theory books go.) – Asaf Karagila Dec 22 '20 at 17:52