Let $A_1,A_2\in L(V,V)$, $A_i(V)=V$ and $\dim\ker A_i=n_i\in\mathbf{N}$. Is $\dim\ker (A_2A_1)=n_1+n_2$ even if $\dim V=\infty$?

Question

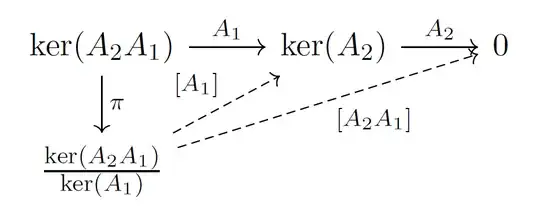
Let $V$ be a vector space that is not necessarly finite dimensional. Consider two surjective linear operators $A_1,A_2\in L(V,V)$ with finite-dimensional kernel: $A_i(V)=V$ and $\dim\ker A_i=n_i\in\mathbf{N}$. Can it be proven that $\dim\ker (A_2A_1)=n_1+n_2$?

In words: Is the dimension of the kernel of the composition of surjective linear operators with finite dimensional kernels the sum of the dimensions of the kernels?

Looking at this formula, one might think that the formula $\dim\ker A_2A_1=n_1+_2$ is valid, but I have looked at the answers and they are based on the rank nullity theorem, which I can't use, since $V$ is not finite dimensional.

Motivation: I want to prove that the solution space of homogeneous linear differential equations of order $n$ is $n$-dimensional by writing the $n$-th order differential operator as composition of first-order differential order with one-dimensional kernel. Actually, the answer to this question completes my proof.

Answer 1

The result is true, and it only requires that $A_1$ is surjective, $A_2$ doesn't have to be.

Suppose that $$\ker A_1=\operatorname{span}\{a_1,\ldots,a_n\},\qquad \qquad\!\!\!\! \ker A_2=\operatorname{span}\{b_1,\ldots,b_m\},$$with $\dim \ker A_1=n$, $\dim\ker A_2=m$. Since $A_1$ is surjective, there exist $x_1,\ldots,x_m$ with $A_1x_k=b_k$. The set $\{a_1,\ldots,a_n,x_1,\ldots,x_m\}$ is linearly independent: if $$\tag1 \sum_j\alpha_j\,a_j+\sum_k\beta_k\,x_k=0, $$ applying $A_1$ we get $\sum_k\beta_kb_k=0$, which gives $\beta_1=\cdots=\beta_m=0$. And then going back to $(1)$ gives us that $\alpha_1=\cdots=\alpha_n=0$.

By construction, $\operatorname{span}\{a_1,\ldots,a_n,x_1,\ldots,x_m\}\subset\ker A_2A_1$. Conversely, if $x\in \ker A_2A_1$, then $A_1x\in\ker A_2$, so there exist $\beta_1,\ldots,\beta_m$ with $$ A_1x=\sum_k\beta_k\,b_k=\sum_k\beta_kA_1x_k=A_1\Big(\sum_k\beta_kx_k\Big). $$ So $x-\sum_k\beta_kx_k\in\ker A_1$, implying that there exist $\alpha_1,\ldots,\alpha_n$ such that $$ x-\sum_k\beta_kx_k=\sum_j\alpha_ja_j, $$ and this shows the reverse inclusion. Thus $\dim\ker A_2A_1=n+m$.

Answer 2

Here's a proof using quotient spaces. We note that the map $[A_1] : V/\ker(A_1) \to V$ induced by $A_1$ is a vector space isomorphism. Thus, $A_2\circ [A_1]:V/\ker(A_1) \to V$ has a kernel with dimension equal to that of $A_2$.

On the other hand, $A_2 \circ [A_1] = [A_2 \circ A_1]$. We note that $$ \ker([A_2 \circ A_1]) = \ker(A_2 \circ A_1)/\ker(A_1) \implies\\ \dim \ker A_2 = \dim \ker([A_2 \circ A_1]) = \dim \ker(A_2 \circ A_1) - \dim \ker(A_1) \implies\\ \dim \ker(A_2 A_1) = \dim \ker A_1 + \dim \ker A_2. $$ To put it another way, we have proved the result with the following commutative diagram:

For those familiar with short exact sequences, this amounts to considering the sequence

$$ 0 \to \ker A_1 \overset{\iota}{\to} \ker A_2A_1 \overset{A_1}{\to} \ker A_2 \overset{A_2}{\to} 0, $$

where $\iota$ denotes the inclusion map.

Answer 3

Here's s solution without too many computations (Martin Argerami's is basically the same). We only need $A_1$ surjective. (or even less, that $\ker(A_2)\subseteq A_1(V)$). We don't actually need finite dimension, and the argument below can be adapted easily.

$$\ker(A_2A_1)=(A_2A_1)^{-1}(0)=A_1^{-1}(A_2^{-1}(0))=A_1^{-1}(\ker(A_2))$$ Choose a basis $\left\{b_1,\ldots,b_n\right\}$ of $\ker(A_2)$. Since $A_1$ is surjective, there are $a_i$ such that $A_1(a_i)=b_i$. Let $W=\operatorname{span}\left\{a_1,\ldots,a_n\right\}$

Clearly, $A_1$ restricts to an isomormorphism from $W$ to $\ker(A_2)$

The usual argument: indeed, the images of the $a_i$ are linearly independet, so the $a_i$ are linearly independent as well, generate $W$, so they form a basis, and $A_1$ takes this basis of $W$ to the basis $\left\{b_1,\ldots,b_n\right\}$ of $\ker(A_2)$, therefore it is an isomorphism. Phew!

Then $A_1(W)=\ker(A_2)$, by construction, and so $A_1^{-1}(\ker(A_2))=W+\ker(A_1)$. Since $A_1$ is injective on $W$ then the spaces $W$ and $\ker(A_1)$ are independent, i.e., $W\cap\ker(A_1)=\left\{0\right\}$, so the sum above is direct: $$\ker(A_2A_1)=A_1^{-1}(\ker(A_2))=W\oplus\ker(A_1)$$ and therefore $$\dim(\ker(A_2A_1))=\dim(W)+\dim(\ker(A_1))=\dim(\ker(A_2))+\dim(\ker(A_1)).$$

---

You can also show that $W\cap\ker(A_1)=\left\{0\right\}$ directly: Suppose $x=\sum_i\lambda_i a_i\in W\cap\ker(A_1)$. Then $$0=A_1(x)=\sum_i\lambda_i A_1(a_i)=\sum_i\lambda_i b_i$$ Since the $b_i$ are linearly independent, all $\lambda_i=0$ and so $x=\sum_i 0a_i=0$.