Find the order of convergence of the Newton-Raphson method from a given table

Question

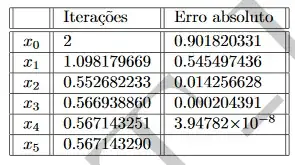
I am given this table

(Iterações = Iterations; Erro absoluto = Absolute Error)

The question is:

Determine the order of convergence of the method from the values of the table and justify.

I got as far a

$$|\alpha - x_{k+1}| \le C|\alpha - x_k|^p \Leftrightarrow \\ \frac{|e(x_{k+1}|}{C} \le |e(x_k)|^p \Leftrightarrow \\ \frac{\log(\frac{|e(x_{k+1}|}{C})}{\log(e(x_k))} \le p$$

That fraction with the logs doesn't look right. How do I know the log on the right hand side isn't negative (thus inverting the sign)?

I don't know how to find C.

Help?

@SimplyBeautifulArt it helped but doesn't quite answer the question... that post was about proving it converges quadratically (you already know the order of convergence and want to prove it). In this case I have to assume I don't know the order of convergence at all. — Segmentation fault, Dec 06 '20 at 16:47
If you use $$\frac{e_{k + 2}}{e_{k + 1}} \sim \frac{e_{k + 1}^p}{e_{k}^p} = \left(\frac{e_{k + 1}}{e_k}\right)^p$$ you can simply isolate $p$. — Mason, Dec 06 '20 at 21:52
@Segmentationfault Let $e_n = |x_n - \alpha|$. Then assume that the iteration $x_n$ satisfies $$e_{n + 1} \sim Ce_n^p$$ for some constants $C$ and $p$, where $f(n) \sim g(n)$ means $\lim_{n \to \infty}\frac{f(n)}{g(n)} = 1$. Then $$e_{n + 2} \sim Ce_{n + 1}^p$$ and $$e_{n + 1} \sim Ce_{n}^p.$$ Dividing the first equation by the second gives the result. — Mason, Dec 06 '20 at 23:43
Welcome to Math.SE! Please use MathJax. For some basic information about writing math at this site see e.g. basic help on MathJax notation, MathJax tutorial and quick reference, main meta site math tutorial and equation editing how-to. — GNUSupporter 8964民主女神地下教會, Dec 07 '20 at 10:46
Please do not use pictures for critical portions of your post. Pictures may not be legible, cannot be searched and are not viewable to some, such as those who use screen readers. Scanned pages from books are discouraged on SE network. Questions should contain sufficient context so that it is answerable with the text alone. — GNUSupporter 8964民主女神地下教會, Dec 07 '20 at 10:47
@GNUSupporter8964民主女神地下教會 I don't think they're exactly a new user, and I don't think there's any issue here. The only image is a table of values which wouldn't be searched for anyways. — Simply Beautiful Art, Dec 07 '20 at 14:40
@Segmentationfault If you read my answer in the dupe carefully, you'll see that the limit$$\lim_{n\to\infty}\frac{\log(\epsilon_{n+1})}{\log(\epsilon_n)}$$gives the order of convergence. You can also derive a similar formula from Mason's suggestions. — Simply Beautiful Art, Dec 07 '20 at 14:43
@SimplyBeautifulArt You're right for the first point. I'll be more careful when I paste the comment from my template next time. The only image here hinders people using screen readers from answering this question. I think you know the syntax of $\rm\LaTeX$ array environment well. — GNUSupporter 8964民主女神地下教會, Dec 07 '20 at 16:28

Find the order of convergence of the Newton-Raphson method from a given table

0 Answers0