If $f_{n}$ has a dense image, then $\bigcap (f_{1}\circ\cdots\circ f_{n})(X_{n})$ is dense

Question

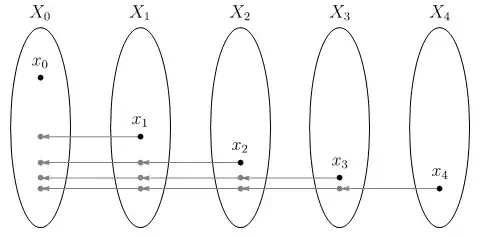
Let $\{(X_{n}, d_{n})\}_{n\in\mathbb{N}}$ be a sequence of complete metric spaces and $\{f_{n}: X_{n}\to X_{n − 1}\}_{n\in \mathbb{N}}$ a sequence of continuous functions. If $f_{n}$ has a dense image for each $n\in \mathbb{N}$, show that $\bigcap_{n\in \mathbb{N}}(f_{1}\circ f_{2}\circ \cdots \circ f_{n}) (X_{n})$ is dense at $X_{0}$.

My attemps: if $f_{n}$ has a dense image then $\overline{f_{n}(X_{n})}=X_{n-1}$ I want to show that $$\overline{\bigcap_{n\in \mathbb{N}}(f_{1} \circ f_{2} \circ \cdots \circ f_{n})(X_{n})} = X_{0}. $$ Let $F_{n}=(f_{1}\circ f_{2} \circ \dots ◦ f_{n})(X_{n})$. By induction, I see that $F_{n+1} ⊆ F_{n} ⊆ X_{0}$. Indeed, if $n=1$, then $$F_{2}=(f_{1}\circ f_{2})(X_{2})=f_{1}(f_{2}(X_{2}))\subseteq f_{1}(\overline{f_{2}(X_{2}}))=f_{1}(X_{1})=F_{1}$$ if we assume that $F_{k+1}\subseteq F_{k}\subset X_{0}$. Then, $$F_{k+2} = (f_{1} \circ f_{2} \circ \cdots \circ f_{k+1} \circ f_{k+2})(X_{k+2}) = (f_{1} \circ f_{2} \circ \cdots \circ f_{k+1})(f_{k+2}(X_{k+2}))\subseteq (f_{1} \circ f_{2} \circ \cdots \circ f_{k+1})(\overline{f_{k+2}(X_{k+2})}) = (f_{1} \circ f_{2} \circ \cdots \circ f_{k+1})(X_{k+1})= F_{k+1}\subseteq F_{k}\subseteq X_{0}$$ from the above we have $$\cdots\subseteq F_{n+1}\subseteq F_{n} \subseteq \cdots \subset F_{2}\subseteq F_{1}$$ then
$$\cdots\subseteq \overline{F_{n+1}}\subseteq \overline{F_{n}} \subseteq \cdots \subset \overline{F_{2}}\subseteq \overline{F_{1}}=X_{0}$$ then $$\overline{\bigcap_{n\in \mathbb{N}}F_{n} }\subseteq \bigcap_{n\in \mathbb{N}}\overline{F_{n}}\subseteq X_{0} .$$

is my reasoning correct?.I've been thinking that Biare's theorem could be used, but I don't know if it's possible since $F_{n}'s$ don't necessarily open.

If it is, how could the other containment prove?. I appreciate any help

Answer 1

I think I found a solution but its rather technical. The following is more of a sketch than a solution with full details.

Let $x_0\in X$ and $\varepsilon>0$ be given.

In a first step, one has to construct points $y_{k,m}$ for $m,k\in\Bbb N_0$ with $k\leq m$ such that $$ \begin{aligned} y_{k,m} &\in X_k \\ y_{0,0} &= x_0 \\ f_k(y_{k,m}) &= y_{k-1,m} \quad\forall m\geq k\geq 1, \\ d_k(y_{k,m},y_{k,m+1}) &< \varepsilon 2^{-m-1} \quad\forall m\geq k\geq 0. \end{aligned} $$ (This requires continuity of these functions and density of the images, and can be done recursively in $m$. This step requires some technical details that I skipped here.) Then, one can show that $\{y_{k,m}\}_{m\geq k}$ is a Cauchy sequence for each $k$. Thus, there exist points $z_k$ with $$ \lim_{m\to\infty} y_{k,m} = z_k \quad\forall k\geq0. $$ Due to continuity of $f_k$, one can show that $f_k(z_k)=z_{k-1}$ holds. Therefore, we have $$ z_0\in F_k \quad\forall k\geq 1 \qquad\text{and therefore}\qquad z_0 \in F_\infty:=\bigcap_{k\in\Bbb N} F_k. $$ Finally, one can also show that $$d_0(z_0,x_0)<\varepsilon$$ holds. Since $\varepsilon>0$ was arbitrary, this shows that $F_\infty$ is dense in $X_0$.

Answer 2

Here is a slight reformulation of @supinf's answer, elucidating the skipped parts:

---

Setting. For $0 \leq i \leq j$, define the function $f^{i\leftarrow j} $ by the composition

$$ X_i \stackrel{f^{i\leftarrow j}}{\longleftarrow} X_{j} \quad = \quad X_i \stackrel{f_{i+1}}{\longleftarrow} X_{i+1} \stackrel{f_{i+2}}{\longleftarrow} \cdots \stackrel{f_j}{\longleftarrow} X_j, $$

i.e.,

\begin{align*} f^{i\leftarrow j} := \begin{cases} f_{i+1} \circ \dots \circ f_{j}, & \text{if $i < j$}, \\ \operatorname{id}_{X_j}, & \text{if $i = j$}. \end{cases} \end{align*}

In particular, note that $f^{j \leftarrow j+1} = f_{j+1}$ and $f^{i\leftarrow j} \circ f^{j \leftarrow k} = f^{i \leftarrow k}$. Using this, OP's question boils down to showing that

$$ \bigcap_{j\geq 0} f^{0\leftarrow j}(X_j) $$

is dense in $X_0$. We establish by showing that in fact the following subset

$$ X^{0\leftarrow} := \biggl\{ z_0 \in X_0 : \text{$\exists$ $\{z_j\}_{j\geq 0} \in \prod_{j\geq 0}X_j$ s.t. $z_j = f_{j+1}(z_{j+1})$ for all $j \geq 0$} \biggr\} $$

is dense in $X_0$.

(Note. It is clear that $X^{0\leftarrow} \subseteq \bigcap_{j\geq 0} f^{0\leftarrow j}(X_j)$. What is not clear to me is whether they coincide or not.)

Proof. Fix any open ball $B(x_0,\epsilon) \subseteq X_0$. Then we construct a sequence $\{x_n\}_{n\geq 0}$ recursively as follows:

Suppose $ x_n \in X_n $ has been chosen. Since $f_{n+1}(X_{n+1})$ is dense in $X_{n}$, we can find a sequence $\{y_k\}_{k\geq 1}$ in $X_{n+1}$ such that

$$\lim_{k\to\infty} f_{n+1}(y_k) = x_{n}.$$

Then for each $j = 0, \dots, n$, by continuity of $f^{j\leftarrow n}$ and $d_j(\cdot, \cdot)$, we have

$$ \lim_{k\to\infty} d_j\bigl( f^{j\leftarrow n}(x_n), f^{j\leftarrow n}(f_{n+1}(y_k)) \bigr) = 0. $$

From this observation, we can pick $x_{n+1} \in X_{n+1}$ so that

$$ d_j\bigl( f^{j \leftarrow n}(x_n), f^{j \leftarrow n+1}(x_{n+1}) \bigr) < \epsilon 2^{-n-1} $$

for each $0 \leq j \leq n$.

Schematically, $x_n$'s are chosen as:

Now we make several observations:

• By the construction, for each $j \geq 0$, the sequence $\{ f^{j\leftarrow n}(x_n) \}_{n = j}^{\infty}$ is Cauchy in $X_j$, and so, $$ z_j := \lim_{n\to\infty} f^{j\leftarrow n}(x_n) $$ exists in $X_j$.

• For each $j \geq 0$, we have $$ z_j = \lim_{n\to\infty} f^{j\leftarrow n}(x_n) = \lim_{n\to\infty} f_{j+1}(f^{(j+1)\leftarrow n}(x_n)) = f_{j+1}(z_{j+1}). $$ In particular, $z_0 \in X^{0\leftarrow}$.

• We have \begin{align*} d_0(x_0, z_0) &= \lim_{N\to\infty} d_0(x_0, f^{0\leftarrow N}(x_N)) \\ &\leq \lim_{N\to\infty} \sum_{n = 0}^{N-1} d_0(f^{0\leftarrow n}(x_n), f^{0\leftarrow n+1}(x_{n+1})) \\ &< \sum_{n = 0}^{\infty} \epsilon 2^{-n-1} \\ &= \epsilon, \end{align*} and so, $z_0 \in B(x_0, \epsilon)$.

This proves that $B(x_0, \epsilon) \cap X^{0\leftarrow} \neq \varnothing$ for any open ball $B(x_0, \epsilon)$ in $X_0$, establishing the desired claim.