Sangaku: to prove one of the intangents is parallel to $BC$

Question

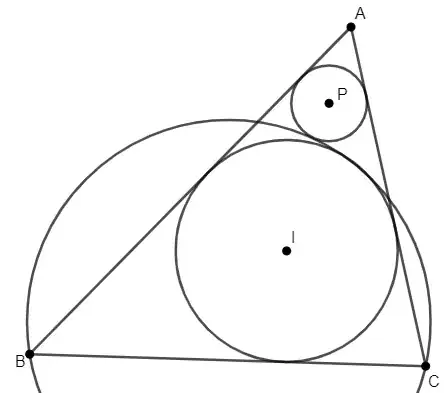
Given an acute triangle $\triangle ABC$ whose incircle is $I(r)$. Let $O(R)$ be the circle through $B$ and $C$ and which touches $I(r)$ interiorly. Show that the circle $P(p)$ which is tangent to $AB$, $AC$ and $O(R)$ (externaly) is such that one intagent line from $P(p)$ and $I(r)$ is parallel to side $BC$.

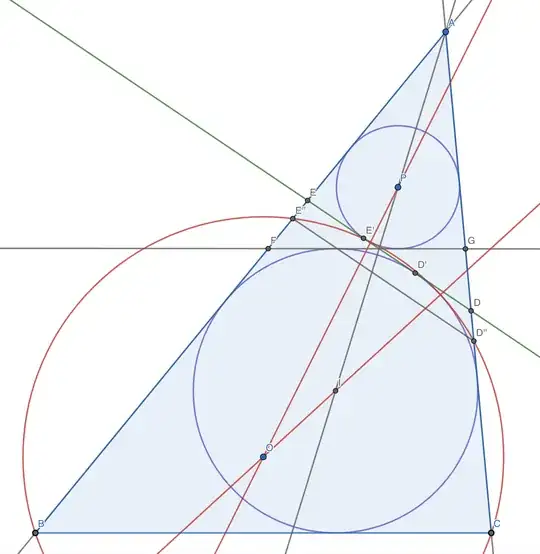
I have seen a couple solutions for this online but I never really understood them and they all seem wrong to me. For example, this is the problem 2 in here. The solution they give doesn't ring a bell. When they say that $\angle ACB - \angle ADE = \angle AED - \angle ABC$ (which is correct) and then they claim that $\angle ADE < \angle ACB$ and $\angle AED > \angle ABC$ imply that $\angle ADE=\angle ABC$ it just sounds wrong. They could just use the congruence of $ADE$ and $AFG$ but instead they use this confuse argument.

And things get worse after the co-axial system. They give a huge jump and conclude that $BCD'E'$ is cyclic. This is best solution I have found for this problem but I just can't agree with it.

Answer 1

The proof of the theorem is simply wrong. It incorrectly asserts that the points of tangency of $\odot O$ with $\odot I$ and $\odot P$ are located at $D'$ and $E'$, respectively. This is impossible, because $DE$ is tangent to $\odot I$ and $\odot P$ at $D'$ and $E'$, respectively, thus if $\odot O$ is tangent to $\odot I$ and $\odot P$ at these same points, $\odot O$ is tangent to line $DE$ at two distinct points--impossible, unless $D' = E'$ which implies $\triangle ABC$ is isosceles. Refer to the figure:

To be precise, the claim presented in the theorem is true; however, the proof is incorrect. If one is not convinced, we can draw the diagram on the Cartesian plane and explicitly calculate the relevant coordinates.

Answer 2

As @Blue has pointed out in the comments,

Ignore the incircle context, and consider disjoint circles $p$ & $q$, with circle $r$ tangent to both (internally, externally, whatever). Then, according to some ugly coordinate-bashing in Mathematica, I believe we can say this: When $r$ meets the external tangents of $p$ & $q$ in four points, two of the resulting chords in $r$ are parallel to the internal tangents of $p$ & $q$; and vice-versa. (The result in question corresponds to a special circumstance where a chord of $r$ happens to be tangent to one of the other circles.)

There's an interesting discussion of this claim at mathoverflow. In particular, this answer cites Gueron's Two Applications of the Generalized Ptolemy Theorem, where it is referred to and proven as the Parallel Tangent Theorem.

Answer 3

Proof

Please consider this messy diagram.

Suppose that the radical axis of $c_1$ and $c_2$ intersects the bigger circle at $O$. From the definition of the radical axis, the tangents from $O$ to $c_1$ and $c_2$, namely $OP$ and $OQ$, are equal in length.

For clarification, $BE,$ $CD,$ $BF,$ $CT$ are the tangents to $c_1$ and $c_2$ as depicted in the picture. Also the internal tangent of those two circles $(\overleftrightarrow{RS})$ intersects the bigger circle at $M$ and $N$.

Now we use Casey's theorem.

First, considering $O,N,c_1,M$ and $O,N,M,c_2$.

$$ON\cdot MR+OM\cdot NR=OP\cdot MN$$ $$ON\cdot MS+OQ\cdot MN=OM\cdot NS$$

Add the two equations,

$$ON\cdot\underbrace{(MR+MS)}_{RS}=OM\cdot\underbrace{(NS-NR)}_{RS}$$ $$\implies ON=OM.$$

That means $O$ is the midpoint of $\overset{\huge\frown}{MN}.$

Similarly, applying Casey's theorem to $O,B,C,c_1$ and $O,B,C,c_2$ we get

$$OC=OB.$$

Therefore $O$ is also the midpoint of $\overset{\huge\frown}{BC}.$

Hence, $NM\parallel BC.$ $~~~\square$