Proof of $\operatorname{arccot}(x)= \arctan(\frac{1}{x})$

Question

$\newcommand{\ac}{\operatorname{arccot}}$ Here is my proof:

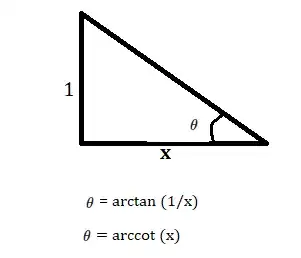
$ \theta = \ac(x)$

$ \cot \theta = x $

$ \displaystyle \tan \theta = \frac{1}{\cot \theta} = \frac{1}{x}$

$ \displaystyle \theta = \arctan \frac{1}{x}$

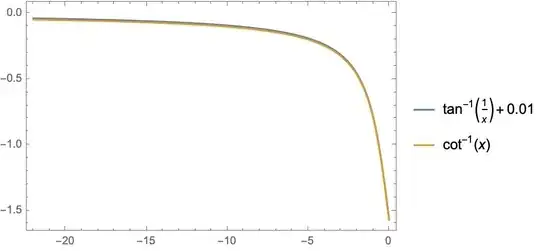
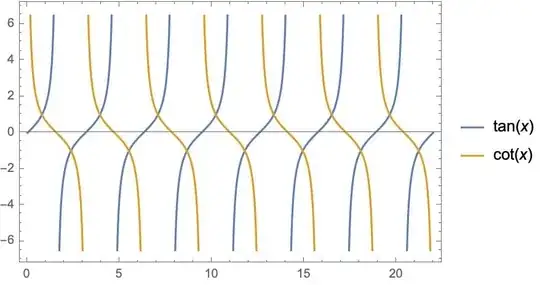
But based on the graph, $\ac(x) = \arctan(\frac{1}{x})$ is only satisfied when $ x > 0$. What is wrong with my proof? What is the error occurred inside a proof?

Are you saying the error lies in the difference of the domain of $cot^-1$ and $tan^-1$? — , Nov 25 '20 at 19:39
There is no such restriction $x>0$. The restriction is $x \ne 0.$ — mjw, Nov 25 '20 at 19:42
Is it because in the above, $cot^-1(x) \in (0, \pi)$ but $tan^-1(\frac{1}{x})$ is only defined in the range $(\frac{-\pi}{2}, \frac{\pi}{2})$? — , Nov 25 '20 at 19:46
yes, thats where the inequality in my previous comment comes from — Anindya Prithvi, Nov 25 '20 at 19:47
@AnindyaPrithvi, That's an arbitrary restriction of the range of $\cot^{-1} x$. — mjw, Nov 25 '20 at 19:47
@mjw not an arbitrary restriction, but a principal value yes. Considering the intent of the OP, the principal value is to be considered — Anindya Prithvi, Nov 25 '20 at 19:48
I guess that we can concede that $\cot^{-1} x = \tan^{-1} x + k\pi$ for some integer $k$. — mjw, Nov 25 '20 at 19:53

score 1 · Answer 1 · answered Nov 25 '20 at 21:15

1

HINT.-Using a figure of a right triangle, it is evident that for $0\lt \theta\lt \dfrac{\pi}{2}$ one has the proposed equality.

from which the equality is true for all $x\gt 0$.

However, for $x\lt0$ the equality is not true because, for example,

$$\operatorname{arccot}(-2)\approx2.6779\\\arctan(-\dfrac 12)\approx-1.1071$$

answered Nov 25 '20 at 21:15

Ataulfo

32,657

1

@Invisible:_ I am sorry. Thank you. – Ataulfo Mar 15 '21 at 14:00

mjw · Answer 2 · 2020-11-25T20:32:08.083

0

There are two conventions for principal value:

$\operatorname{arccot} x \in (-\pi/2, \pi/2]$ with a discontinuity at zero.
$\operatorname{arccot} x \in (0, \pi)$

See https://mathworld.wolfram.com/InverseCotangent.html

It turns out that $\operatorname{arccot} x = \arctan(1/x)$ for all $x\ne 0$ for one convention of principal value.

If you want to adapt or enforce a particular range for $\operatorname{arccot} x$, then $\operatorname{arccot} x = \arctan(1/x) + k \pi$ for some integer $k$.

Here is what Mathematica thinks:

 Plot[{ArcTan[1/x] + .01, ArcCot[x]}, {x, -7 Pi, 0}, Frame -> True, 
  PlotRange -> All]

You can rotate this second plot $90^\circ$ and define your range anyway you want up to a multiple of $\pi.$

edited Nov 25 '20 at 20:32

answered Nov 25 '20 at 19:48

mjw

8,813

I'm sorry, but how do I interpret this graph? – Nov 25 '20 at 19:49
Added a legend. – mjw Nov 25 '20 at 19:50
Added $0.01$ to the $\tan^{-1}(1/x)$ curve to show that there are two curves there! – mjw Nov 25 '20 at 19:50
@ext_vayne The inverse function is multivalued outside the principal domain/range...so the cottangent and tangent overlap – Anindya Prithvi Nov 25 '20 at 19:50

score 0 · Answer 3 · answered Mar 14 '21 at 12:38

Long comment:

The first problem with $$\arctan\left(\frac1x\right)=\operatorname{arccot}(x)$$ is that $\arctan$ is an odd function, while $\operatorname{arccot}$ isn't.

Indeed, $\forall x\in\Bbb R$, the following holds:

$$\arctan(x)+\operatorname{arccot}(x)=\frac\pi2\implies\operatorname{arccot}(x)=\frac\pi2-\arctan(x)$$ Hence, if $x>0$, then $$\arctan\left(\frac1{-x}\right)=-\arctan\left(\frac1x\right)=-\operatorname{arccot}(x)=-\operatorname{arccot}(-(-x))$$ and we cannot just move the sign under the argument. Therefore, $$\arctan\left(\frac1x\right)=\begin{cases}-\operatorname{arccot}(-x), &x<0\\\operatorname{arccot}(x),&x>0\end{cases}$$

Proof of $\operatorname{arccot}(x)= \arctan(\frac{1}{x})$

3 Answers3

Long comment:

Linked