Actually this is not so hard to do with Paley-Zygmund. Not sure why I didn't see this before. We just substitute $X$ by $e^{s X}$ like in Chernoff's bound:
$$
\Pr[e^{sX} > \theta E[e^{sX}]]
= \Pr[X > \log(\theta E[e^{sX}])/s]
\ge (1-\theta)^2\frac{E[e^{s X}]}{E[e^{2 s X}]}.
$$
For an example with the normal distribution, where $E[e^{s X}]=e^{s^2/2}$ we get
$$
\Pr[X > \log(\theta)/s + s/2]
\ge (1-\theta)^2 e^{-\tfrac{3}{2}s^2},
$$
so taking $\log(\theta)/s+s/2=t$ and $\theta=1/2$ we get
$$
\Pr[X > t]
\ge \frac{1}{4} e^{-\left(\sqrt{t^2+\log (4)}+t\right)^2} \sim e^{-6t^2}.
$$
Indeed, the value of $\theta$ matters very little.
We can compare this result to the true asymptotics for the normal distribution
$
\Pr[X > t] \sim e^{-t^2/2}
$ to see that we lose roughly a factor 12 in the exponent.
Alternatively for $t\to0$ we get $\Pr[X>0]\ge1/16$.
We can improve the lower bound a bit to $\sim t^{O(1)} e^{-2t^2}$ using the $L^p$ version of Paley-Zygmund, but there's still a gap.
This differs from the situation of the upper bound (Markov/Chernoff) which is tight in the exponent.
If there's a way to get a tight exponent using moment generating functions, I'm still very interested.
Edit: Just to clarify what I mean by $L^p$ PZ, it is the following inequality:
$$
\operatorname{P}( Z > \theta \operatorname{E}[Z \mid Z > 0] )
\ge \left(\frac{(1-\theta)^{p} \, \operatorname{E}[Z]^{p}}{\operatorname{E}[Z^p]}\right)^{1/(p-1)}.
$$
Using the same substitution as before, and defining $m(s)=E[e^{s X}]$, we get:
$$
\Pr[X > \log(\theta m(s))/s]
\ge \left((1-\theta)^{p}\frac{m(s)^p}{m(s p)}\right)^{1/(p-1)}.
$$
In the limit $p\to 1$ we can Taylor expand as
$$
\left(\frac{m(s)^p}{m(s p)}\right)^{1/(p-1)}
= m(s)\,\exp\left(- \frac{s m'(s)}{m(s)} + O(p-1)\right),
$$
which is nice, as $m(s)\exp(- \frac{s m'(s)}{m(s)}) = e^{-s^2/2}$ for the normal distribution.
However, this lower bound is only for $X\ge \log(\theta)/s+s/2$, not $X \ge s$.
So even if we let $s\to\infty$ and ignore the $(1-\theta)^{p/(p-1)}$ factor, we still only get the lower bound $\Pr[X\ge t] \ge e^{-t}$.
So we still don't even get the exponential factor right.
More thoughts:
It's interesting that Chernoff gives you (define $\kappa(s)=\log Ee^{s X}$)
$$
\Pr[X \ge t] \le \exp(\kappa(s) - s t),
$$
while PZ gives you (modulo some constants related to $\theta$),
$$
\Pr[X \ge \kappa(s)] \ge \exp(\kappa(s) - s \kappa'(s)),
$$
by the arguments above.
For Chernoff, the optimal choice of $s$ is st. $\kappa'(s)=t$.
For PZ we need $\kappa(s)=t$.
So they meet for distributions where $\kappa'(s)=\kappa(s)$, meaning $Ee^{sX}=e^{e^s}$.
The Poisson distribution is roughly an example of this.
Update: Using Cramér's method
Usually, Chernoff is proven sharp using Cramér's theorem. Cramér considers a sum of IID rvs., but I thought I should really see what happens in the general case.
Define $m(t)=E[e^{t X}]$ and $q_t(x) = e^{x t} m(t)^{-1} p(x)$
\begin{align*}
\Pr[X > s]
&= \int_s^\infty p(x)
\\&= m(t) \int_s^\infty e^{-t x} q_t(x)
\\&\ge m(t) \int_s^{s+\varepsilon} e^{-t x} q_t(x)
\\&\ge m(t) e^{-t (s+\varepsilon)} \int_s^{s+\varepsilon} q_t(x).
\end{align*}
We set $t\ge 0$ such that $E[Q]=\kappa'(t)=s+\varepsilon/2$.
Then by Chebyshev's inequality,
\begin{align*}
\int_s^{s+\varepsilon} q_t(x)
&= \Pr[|Q-\mu| \le \varepsilon/2]
\\&\ge 1-\kappa''(t)/(\varepsilon/2)^2.
\end{align*}
We set $\varepsilon=2\sqrt{2\kappa''(t)}$.
Putting it together, we have proven the lower bound
\begin{align*}
\Pr[X > s]
&\ge \tfrac12 \exp\left(\kappa(t) - (s+\varepsilon)t\right),
\end{align*}
where $t=\kappa'^{-1}(s+\varepsilon/2)$.
\subsection{Example}
To understand the bound we are aiming for, let's do a Chernoff bound,
\begin{align*}
\Pr[X > s]
=\Pr[e^{tX} > e^{ts}]
\le e^{\kappa(t)-ts},
\end{align*}
which we minimize by setting $\kappa'(t)=s$.
For $X$ normal distributed, we have
$\kappa(t)=t^2/2$,
$\kappa'(t)=t$, and
$\kappa''(t)=1$.
So the upper bound is
[
\Pr[X > s] < \exp(-s^2/2).
]
The lower bound from before gives us
\begin{align*}
\Pr[X > s]
&\ge \tfrac12 \exp\left(t^2/2 - (s+\varepsilon)\right),
\\&= \tfrac12 \exp\left(-s^2/2 - \varepsilon s - 3\varepsilon^2/8\right).
\end{align*}
It would be nice to replace $\exp(-\varepsilon s)$ with something
polynomial, like $1/s^2$, but at least we get the leading coefficient right.
Improving Cramér:
The main loss we get is from $e^{t(s+\varepsilon)}$.
Let's see if we can avoid it.
With the above bound we actually get
\begin{align*}
\Pr[X > s]
&= \int_s^\infty p(x)
\\&= e^{\kappa(t)} \int_s^\infty e^{-t x} q_t(x)
\\&\ge e^{\kappa(t)}
e^{-(\frac{\sigma^2}{\mu-s}+(\mu-s))t}\frac{(\mu-s)^2}{\sigma^2+(\mu-s)^2}.
\end{align*}
The last inequality comes from the inequality
$$
[x > s] e^{-t x}
\ge \frac{e^{-t x_0}}{(x_0 - s)^2} (x - s) (-s - x + s t x + 2 x_0 - t (s + x) x_0 + t x_0^2)
$$
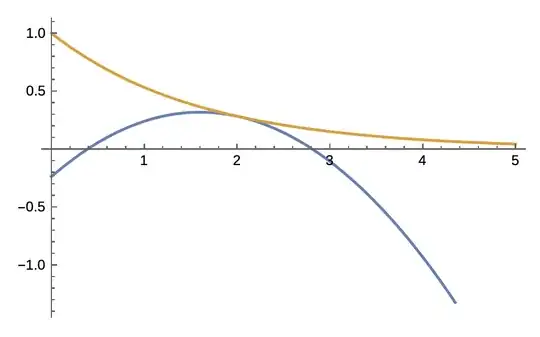
That is, we place a quadratic under the curve $\exp(-t x)$ such that it has a root at $x=s$.
We pick
$$x0=\frac{\sigma^2-\mu s+\mu^2}{\mu-s} = \frac{\sigma^2}{\mu-s} + \mu,$$
where $\mu=E[Q]=k'(t)$ and $\sigma^2 = E[(Q-\mu)^2]=k''(t)$.
This method gives us
\begin{align*}
\Pr[X > s]
\ge \frac{\mu-s}{x_0-s} \exp(\kappa(t) - x_0t)
\end{align*}
At least asymptotically, it seems correct to choose $k'(t) = s + \sigma = s + \sqrt{k''(t)}$. Using that choice we get
\begin{align}
\Pr[X \ge s] \ge \frac{1}{2} \exp(k(t) - ts - 2t\sqrt{k''(t)}).
\end{align}
In the normal distributed case of $\kappa(t)=\mu t + \sigma^2 t^2/2$
and $\kappa'(t)=\mu+\sigma^2 t$ and $\kappa''(t)=\sigma^2$
we can take $t \sigma^2 = s - \mu/2 + \sqrt{\mu^2-4\sigma^2}/2$ to get
$$
Pr[X\ge \exp(-s^2/(2\sigma^2) + O(1)).
$$
The bound $\frac12 e^{\kappa(t)-ts-2\kappa''(t)t}$ is a bit prettier than what we had before, but not much better.
We still get that if $s>\!>\sigma$, it's tight, but for $s=O(\sigma)$ it's not.
Here is a figure of what I mean by placing a quadratic under the exponential: